Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.6 - Ex. 20

(a) Trace as cônicas

para e vários valores de . Como o valor de afeta o formato da cônica?

(b) Trace essas cônicas para e vários valores de . Como o valor de afeta o formato da cônica?

Passo 1

Bom, pessoal. Vamos traçar as cônicas para e vários valores de . A equação fica assim:

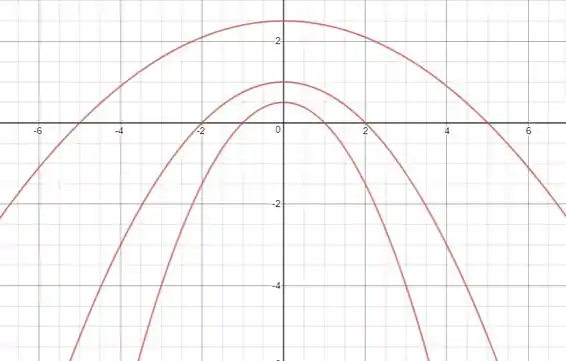
À medida que cresce, o vértice da parábola também vai subindo, e seu formato vai ficando cada vez mais “aberto”.

Passo 2

(b) Para , a equação fica assim:

Agora vamos traçar as cônicas para vários valores de , beleza?

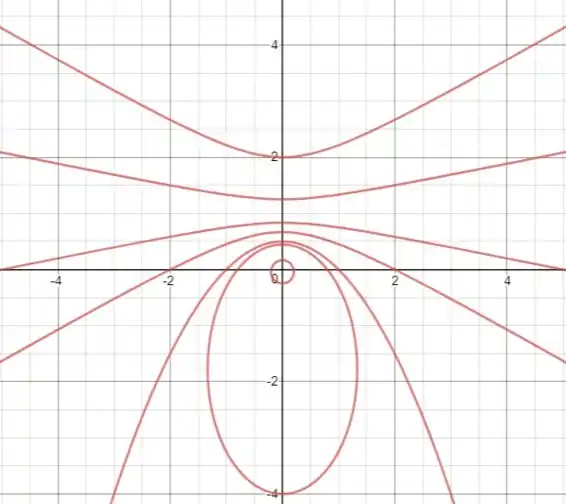
Repare que, quando cresce entre e , a cônica é uma elipse que vai ficando mais achatada. Quando , a cônica é uma parábola. Quando vai crescendo acima de , a cônica é uma hipérbole que vai ficando mais “aberta”.

Resposta

(a) Quanto maior o valor de , mais “aberta” é a parábola.

(b) À medida que cresce, a cônica passa de elipse a parábola, e de parábola a hipérbole, com curvas cada vez mais abertas.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 1 + 2 sen ⁡ ( θ / 2 ) (nefroide de Freeth)

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 2 - 5 sen ⁡ ( θ / 6 )

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = e sen ⁡ θ - 2 cos ⁡ ( 4 θ ) (curva em borboleta)

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = sen 2 ⁡ ( 4 θ ) + cos ⁡ ( 4 θ )

Use uma ferramenta gráfica para traçar a curva polar. Escolha o intervalo do parâmetro para ter certeza de que você fez a curva inteira. r = 1 - 0,8 sen 2 ⁡ θ (hipopédia)