Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 43

Calcule a integral, transformando para coordenadas esféricas.

∫ - 2 2 ∫ - 4 2 - y 2 4 2 - y 2 ∫ - 4 2 - y 2 - x 2 4 2 - y 2 - x 2 x 2 + y 2 + z 2 3 2 d z d x d y

Passo 1

Faaaala meu povo, tudo bem!? Vamos começar!

Nesse exercício, devemos calcular a integral abaixo a transformando em coordenadas esféricas:

��� - 2 2 ∫ - 4 2 - y 2 4 2 - y 2 ∫ 2 - 4 - y 2 - x 2 2 + 4 - y 2 - x 2 x 2 + y 2 + z 2 3 2 d z d x d y

Vish, e agora? Calma, juntos vamos desvendar essa!!

O primeiro passo é lembrar como é escrito em coordenadas esféricas. Veja abaixo:

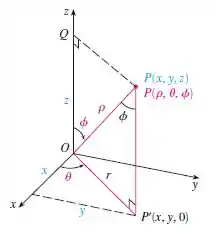
Lembre-se que em coordenadas esféricas o d V = d x d y d z , fica:

d V =   ρ 2 sin ⁡ ϕ d ρ   d ϕ   d θ

Agora devemos olhar para os limites de integração, e repare nos limites da variável z :

2 - 4 - y 2 - x 2 ≤ z ≤ 2 + 4 - y 2 - x 2

Dessa relação temos que:

z = 2 + 4 - y 2 - x 2

Se elevarmos ambos os lados ao quadrado e isolar todas as variáveis de um lado da igualdade e números do outro, vamos obter a expressão de uma esfera de raio 2 . Vou deixar para você demonstrar isso agora, e praticar!

Como não tem nenhuma restrição que a esfera está em um quadrante ou octante especifico, consideramos a variação de ângulo para uma esfera completa. Logo temos:

0 ≤ ρ ≤ 2 0 ≤ θ ≤ 2 π 0 ≤ ϕ ≤ π

Agora é só você substituir as variáveis em coordenadas esféricas no integrando:

x 2 + y 2 + z 2 3 2

Feito isso, é só montar sua integral com os limites e resolvê-la.

Bora lá!!!

Passo 2

Vamos relembrar a integral que queremos passar para coordenadas esféricas:

∫ - 2 2 ∫ - 4 2 - y 2 4 2 - y 2 ∫ 2 - 4 - y 2 - x 2 2 + 4 - y 2 - x 2 x 2 + y 2 + z 2 3 2 d z d x d y

Olhando para os intervalos de z , temos:

2 - 4 2 - y 2 - x 2 ≤ z ≤ 2 + 4 2 - y 2 - x 2

Podemos dizer que:

z = 2 + 4 - y 2 - x 2

Isolando as variáveis de um lado obtemos:

( z - 2 ) 2 +   y 2 + x 2 = 2 2

Veja que é exatamente uma esfera de raio 2 . Assim, sabendo que não a nenhuma restrição no enunciado, temos uma esfera completa. Logo os intervalos serão:

0 ≤ ρ ≤ 2 0 ≤ θ ≤ 2 π 0 ≤ ϕ ≤ π

Passo 3

Então, já sabemos os intervalos de integração em coordenadas esféricas. Agora precisamos transformar o integrando nessas coordenadas:

x 2 + y 2 + z 2 3 2

Bom, sabemos que as relações de transformação em coordenadas esféricas são:

x = ρ s e n ϕ c o s θ y = ρ s e n ϕ s e n θ z = ρ c o s ϕ

Sendo assim o integrando fica desse jeito, saca só:

ρ s e n ϕ c o s θ 2 + ρ s e n ϕ s e n θ 2 + ρ c o s ϕ 2 3 2

Simplificando temos:

ρ 2 s e n 2 ϕ s e n 2 θ + cos 2 ⁡ θ + ρ 2 cos 2 ⁡ ϕ 3 2

Utilizando da relação trigonométrica:

s e n 2 x + cos 2 ⁡ x = 1

Vamos ter que:

ρ 2 s e n 2 ϕ + ρ 2 cos 2 ⁡ ϕ 3 2

ρ 2 s e n 2 ϕ + cos 2 ⁡ ϕ 3 2

Novamente utilizando a relação trigonométrica, concluímos que:

x 2 + y 2 + z 2 3 2 = ( ρ 2 ) 3 2 = ρ 3  

E o d V ? Em coordenadas esféricas temos:

d V = ρ 2 s e n ϕ   d ρ   d ϕ   d θ

Agora é só substituir tudo isso na integral e resolver! Bora lá?

Passo 4

Substituindo, vamos ter a seguinte integral:

∫ 0 2 π ∫ 0 π ∫ 0 2 ( ρ 3 ) ρ 2 s e n ϕ   d ρ   d ϕ   d θ

∫ 0 2 π ∫ 0 π ∫ 0 2 ρ 5 s e n ϕ   d ρ   d ϕ   d θ

Agora vamos começar a integrar. Lembra que começamos integrando de dentro para fora, e tudo que não depende da variável de integração é uma constante.

Integrando em d ρ , vamos ter:

∫ 0 2 π ∫ 0 π ρ 6 6 0 2 s e n ϕ d ϕ   d θ

Aplicando os limites de integração temos:

2 6 6 ∫ 0 2 π ∫ 0 π s e n ϕ d ϕ   d θ

Passo 5

Agora restou fazer as integrações nos ângulos ϕ e θ :

32 3 ∫ 0 2 π ∫ 0 π s e n ϕ d ϕ   d θ

Integrando em d ϕ , temos:

32 3 ∫ 0 2 π - c o s ϕ 0 π d θ

Aplicando os limites de integração, temos:

32 3 ∫ 0 2 π - cos ⁡ π - cos ⁡ 0 0 π d θ

Sabemos que:

cos ⁡ π = - 1

cos ⁡ 0 = 1

Vamos ter que:-

32 3 ∫ 0 2 π - ( - 1 - 1 ) d θ

64 3 ∫ 0 2 π d θ

Por fim, integrando em d θ :

64 3 ( θ ) 0 2 π

Aplicando os limites de integração:

64 3 ( 2 π )

Logo, nossa resposta é:

128 π 3  

Resposta

128 π 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Utilize as coordenadas esféricas.Calcule ∭ B x 2 + y 2 + z 2 d V , onde B é a bola unitária x 2 + y 2 + z 2 ≤ 1 .
Determine o volume do sólido que está acima do cone ϕ = π / 3 e abaixo da esfera ρ = 4 cos ⁡ ϕ .
Encontre desigualdades que descrevam uma bola oca com diâmetro de 30 cm e espessura de 0,5 cm. Explique como você posicionou o sistema de coordenadas que escolheu.Suponha que a bola seja cortada pela
Calcular ∭_T^() ( x^2 + y^2 + z^2 ) . d V , onde T é a esfera x^2 + y^2 + z^2 = 9 .
Calcular ∭ T d V , onde T é a casca esférica delimitada por x 2 + y 2 + z 2 = 9 e x 2 + y 2 + z 2 = 16