Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.3 - Ex. 18
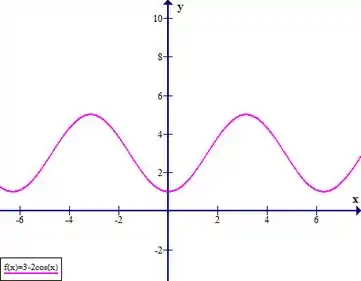
Faça o gráfico da função à mão, não usando pontos, mas a partir dos gráficos de uma das funções padrão dadas na seção 1.2, e então aplique as transformações apropriadas.
Passo 1
Eaee, belezinha?? Bom... O enunciado nos dá a seguinte função:
Queremos plotar o gráfico dessa função a partir dos gráficos de uma das funções padrão dadas na seção 1.2.
Nesse sentido, iremos procurar alguma função dessa seção eu se assemelhe com a nossa e aí a gente vai verificando as diferenças e analisando o que elas significam no gráfico.
Bora lá?? 😉
Passo 2
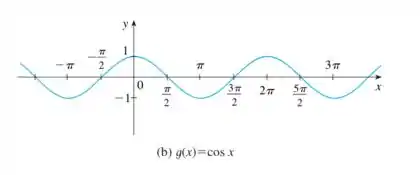
Bom pessoal, esta função é do tipo trigonométrica.
De acordo com a figura 18 da Seção 1.2, podemos ver como o gráfico da função cosseno:
Porém, na nossa função , temos um coeficiente de sinal negativo multiplicando a função , além da soma por unidades.
Nesta seção 1.3, aprendemos que quando temos uma função do tipo devemos alargar a função na vertical.
Como temos ainda um sinal negativo devemos espelhar esta função em relação ao eixo .
Ainda temos o tipo em que devemos deslocar a função para cima do gráfico em .
Unindo as características acima, temos:
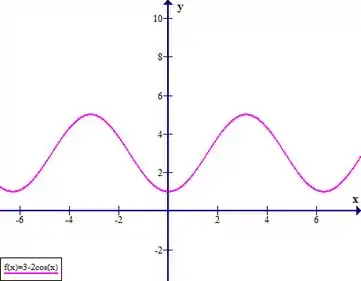
Resposta
