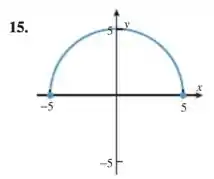
Conforme vimos no Exemplo 3, a equação não define como uma função de . Cada gráfico nestes exercícios é uma porção do círculo . Em cada caso, determine se o gráfico define como uma função de e, se isso ocorrer, dê uma fórmula para em termos de .

Opa, vamos lembrar como é a definição!

Se uma variável depende de uma variável de tal modo que cada valor de determina exatamente um valor de , então dizemos que é uma função de

Ou seja, para cada valor de só podemos ter um valor de

Show, nessse caso a gente consegue ver que para cada valor de só temos um valor de

Vamos escrever isso em relação a , temos que:

Mas isso é para a circunferência inteira, como a gente ta só com a parte de cima, ficamos com: