Esboce o gráfico da equação para n=1,3 e 5 em um sistema de coordenadas e para n=2, 4, e 6 em outro sistema de coordenadas. Confira seu trabalho com um recurso gráfico.
(a)
(b)
(c)
Passo 1
Cara, infelizmente, não consigo te mostrar um esboço meu kkk, mas vou te dizer como eu faria e a gente confere aqui com o recurso gráfico, ok?
A gente precisa ter umas funções em mente, que vão servir de base para a nossa comparação. Elas serão identificadas pela família da função que queremos.
Por exemplo em (a) .
Para ímpar, no nosso caso, e , vamos comparar à função , com exceção de que vamos comparar a . Pois é ímpar também.
Então, a partir de , qual a modificação que fizemos? Multiplicamos por , ficando , que seria o gráfico de alongado num fator de pelo eixo :
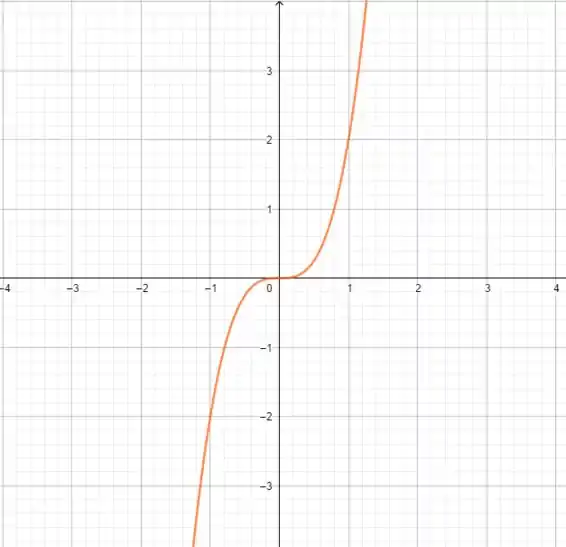
E qual a diferença de para ? O achatamento da função, apenas! Então, o gráfico de é o de , só que mais achatado:
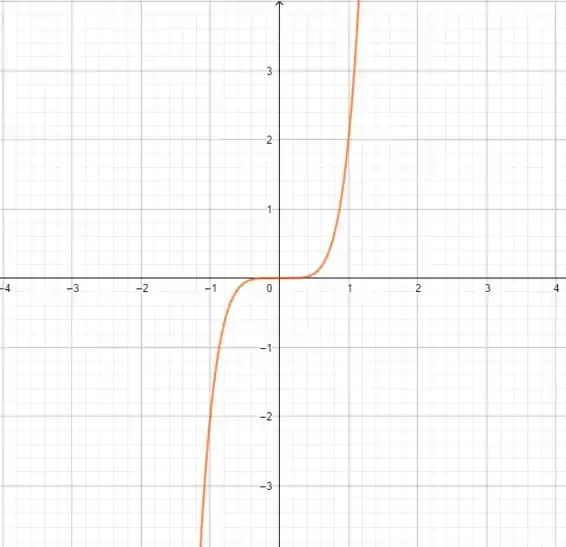
Por último, quando . E, partindo de , temos apenas uma multiplicação por , o que nos dá um alongamento num fator de de pelo eixo :
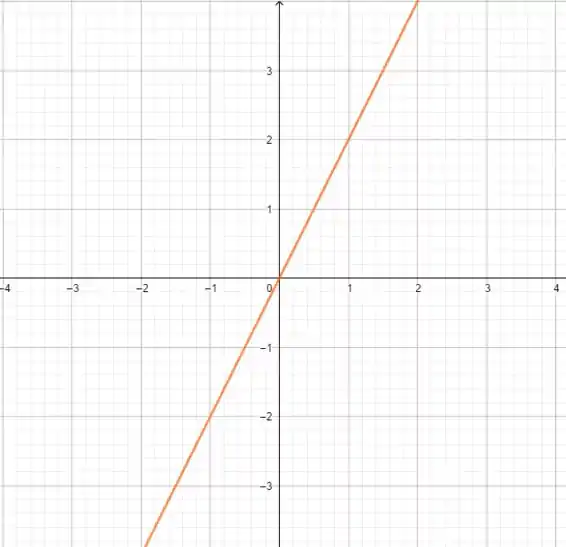
Passo 2
Para par, ou seja, e , vamos fazer a comparação com , pois é par também.
Dessa forma, partindo de , a diferença para a nossa função é a multiplicação por , o que nos dá um alongamento num fator de de pelo eixo . Além disso, a diferença entre os gráficos com , e será apenas o achatamento também, quanto maior a potência, maior o achatamento!!
Dessa forma, :
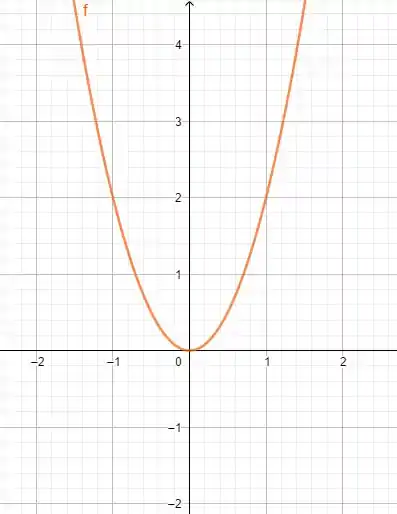
Para :
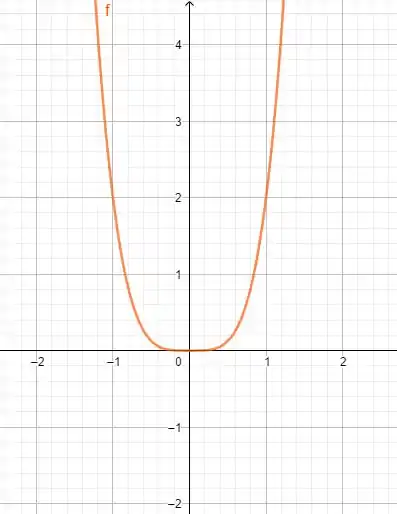
Para :
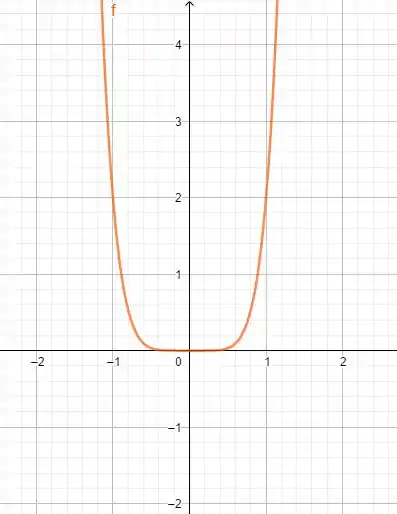
Passo 3
(b)
Agora, temos uma função da família . Para os valores ímpares, vamos comparar com , a diferença entre os valores de será o achatamento. O único diferente é o , que tem a comparação com .
Para os valores pares, a comparação será com . A diferença, de novo, é no achatamento.
Para todos os gráficos, por temos a multiplicação por na função, isso reflete o gráfico num pelo eixo .
Passo 4
Então, para :
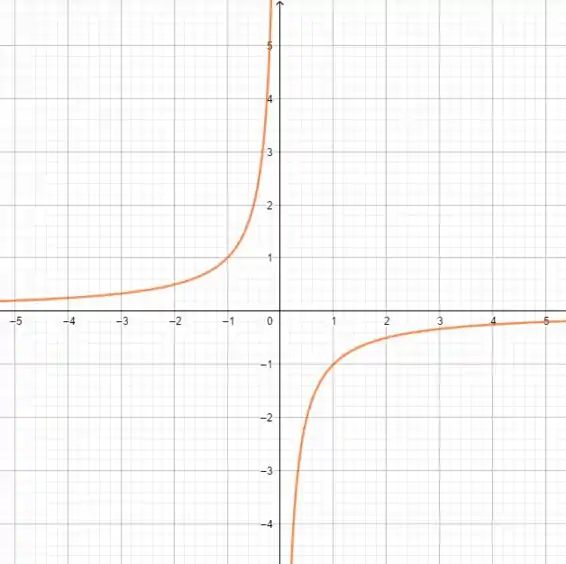
Para :
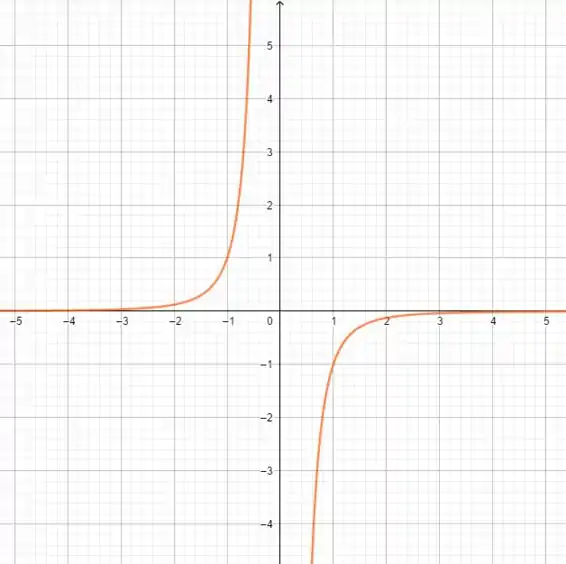
Para :
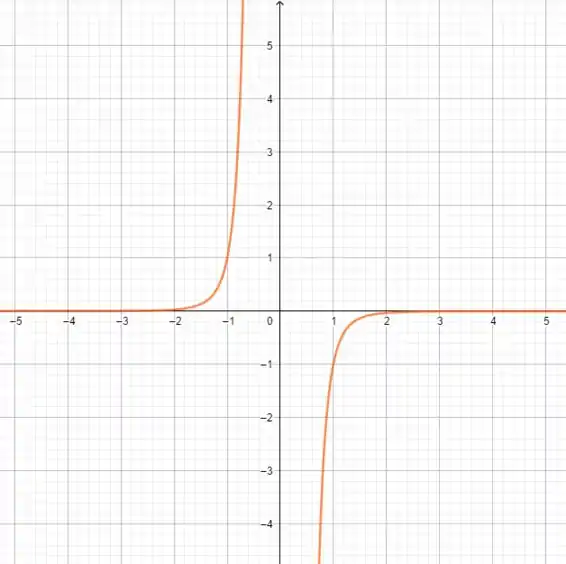
Para :
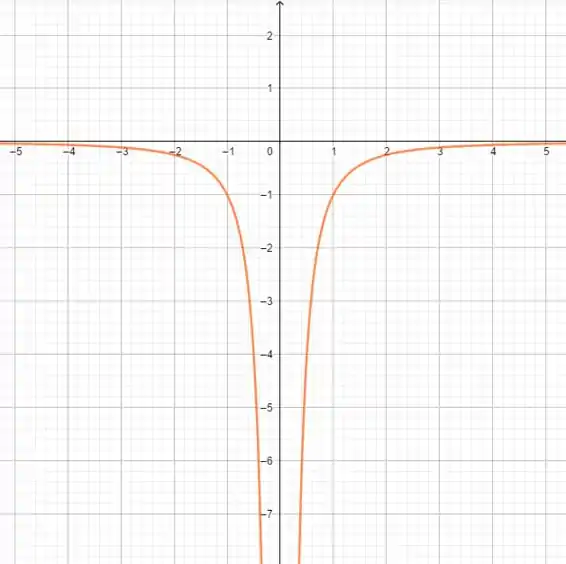
Para :
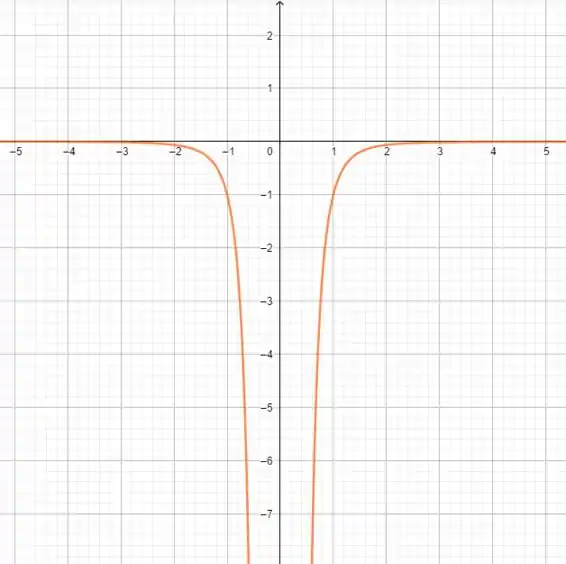
Para :
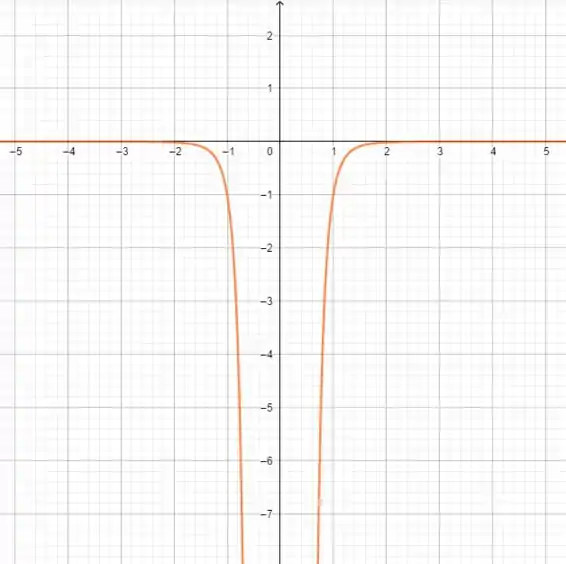
Passo 5
(c)
Arrumando:
Vamos comparar à família de , onde teremos um deslocamento dos gráficos em duas unidades para a esquerda, por conta da soma por no . Além da reflexão por pela multiplicação pelo e alongamento num fator de pelo eixo , por conta da multiplicação por .
E a diferença entre os pares e ímpares é o domínio: para par, teremos o gráfico para valores positivos de , para ímpar, teremos o gráfico para todos os valores de .
Além disso, a diferença entre as potências continua sendo o achatamento da curva e para , teremos , que é a reta deslocada em seis unidades para a esquerda, a reflexão por e o alongamento num fator de pelo eixo .
Passo 6
Então, para :
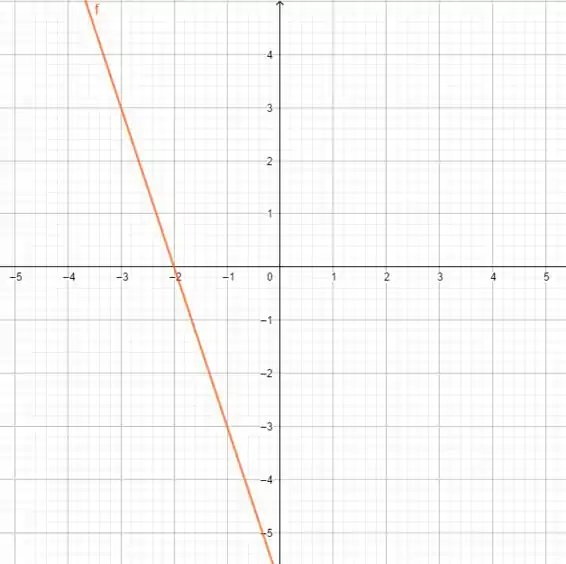
Para :
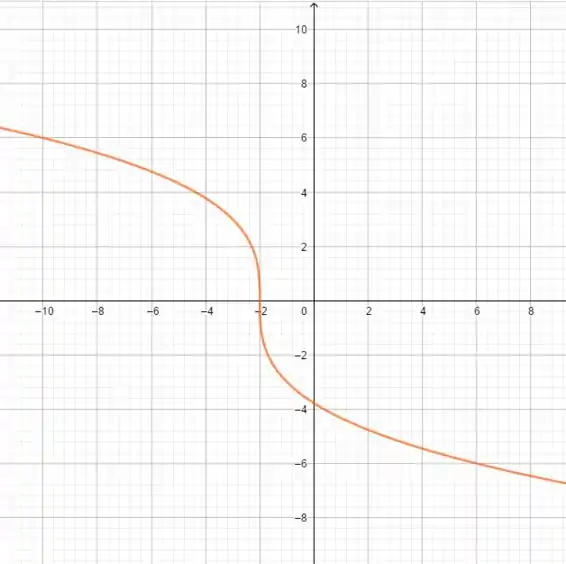
Para :
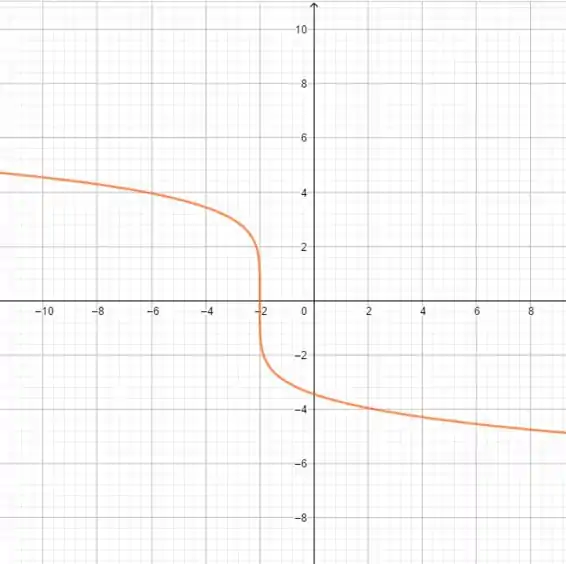
Para :
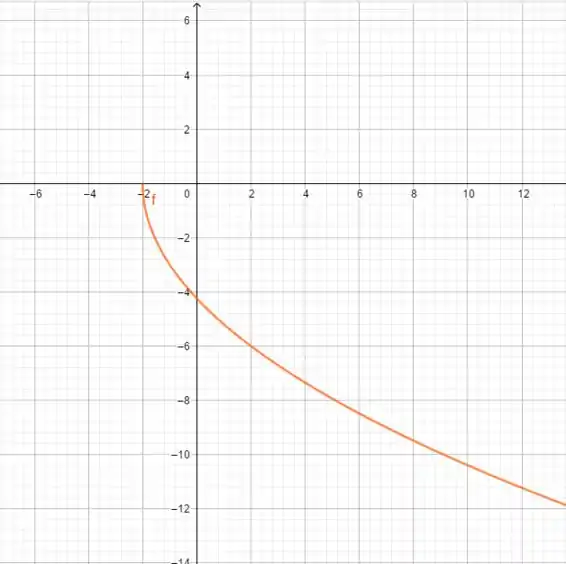
Para :
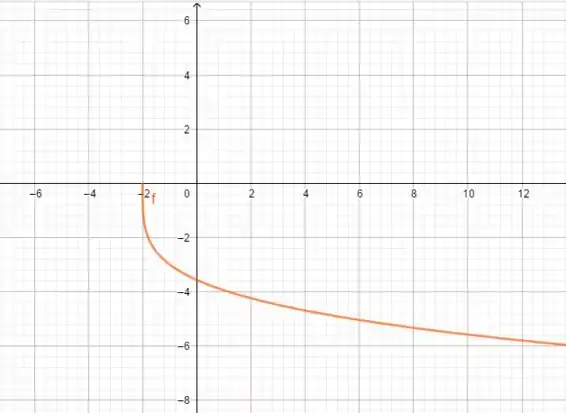
Para :
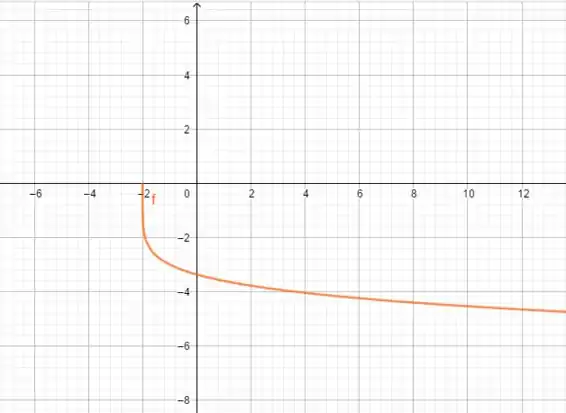
Resposta
Explicação no passo a passo.