Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 3.3 - Ex. 24

Considere o problema de valor inicial

5 u ' ' + 2 u ' + 7 u = 0 ,       u 0 = 2 ,       u ' 0 = 1

  1. Encontre a solução de u ( t ) deste problema.
  2. Encontre o menor T para o qual u t ≤ 0,1 para todo t > T

Passo 1

O começo da nossa seção 3.3, temos uma equação geral dada por a y ' ' + b y ' + c y = 0 , onde a , b e c são números reais. Supondo como solução y = e r t , é possível descrever a nossa solução geral.

Passo 2

(a) Usando a ideia do passo 1, temos que

5 u ' ' + 2 u ' + 7 u = u ' ' + 2 5 u ' + 7 5 u = r 2 e r t + 2 5 r e r t + 7 5 e r t = 0

Na qual temos que u ' ' = r 2 e r t e u ' = r e r t .

Assim temos nossa equação característica dada por

r 2 + 2 5 r + 7 5 = 0

Agora só precisamos resolver nossa equação de segundo grau. Lembra de Baskara? Tem gente que acha que não serve pra nada hahaha. Resolvendo nossa equação chegamos em

r = - 1 ± 34 i 5

Tendo como solução

u ( t ) = e - t 5 c 1 e 34 5 i t + c 2 e - 34 5 i t

Ou

u t = e - t 5 C 1 cos ⁡ 24 5 t + C 2 sin ⁡ 34 5 t

Passo 3

Uma vez que encontramos a nossa solução, podemos agora resolver nosso problema de valor inicial. Assim teremos que

u 0 = C 1 = 2

E tomando a derivada

u ' t = - e - t / 5 5   C 1 cos ⁡ 34 5 t + C 2 sin ⁡ 34 5 t + e - t 5 24 5 - C 1 sin ⁡ 34 5 t + C 2 cos ⁡ 34 5 t

Onde em u ' 0 = 1 , ou seja

u ' 0 = - 1 5 2 + C 2 ⋅ 0 + 34 5 - 2 ⋅ 0 + C 2 = 1

- 2 5 + 34 5 C 2 = 1 → C 2 = 7 34

Desta forma nossa solução geral se torna

y ( t ) = e - t 5 2 cos ⁡ 34 5 t + 7 34 sin ⁡ 34 5 t

Passo 4

(b) Agora queremos saber quando u t = 0,1 , ou seja

e - t 5 2 cos ⁡ 34 5 t + 7 34 sin ⁡ 34 5 t ≤ 0,1

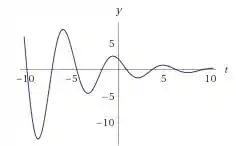
Onde graficamente memos que u t ≤ 0,1 se da em T = 14,5115

Resposta

  1. y ( t ) = e - t 5 2 cos ⁡ 34 5 t + 7 34 sin ⁡ 34 5 t
  2. 14,5115
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Indicamos, neste problema, um procedimento 7 diferente para resolver a equação diferencial y ' ' + b y ' + c y = D 2 + b D + c y = g ( t ) em que b e c são constantes, e D denota diferenciação em rela
Em cada um dos Problemas de 36 a 39, use o método do Problema 35 para resolver a equação diferencial dada. y ' ' + 2 y ' + y = 2 e - t
Nos problemas 1-26, resolva a equação diferencial dada pelo método dos coeficientes indeterminados.2. 4 y ' ' + 9 y = 15
Nos problemas 1-26, resolva a equação diferencial dada pelo método dos coeficientes indeterminados.9. y ' ' - y ' = - 3
Nos problemas 1-26, resolva a equação diferencial dada pelo método dos coeficientes indeterminados.12. y ' ' - 16 y = 2 e 4 x