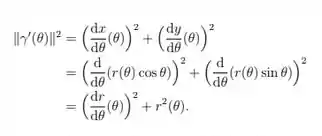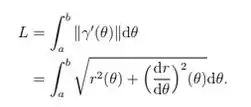Exercícios de Parametrizações com Geometria - Lista de Exercícios Resolvida
Questão 1
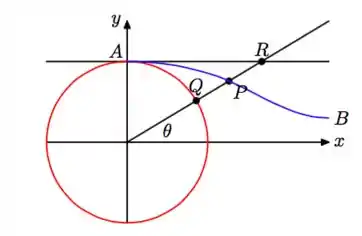
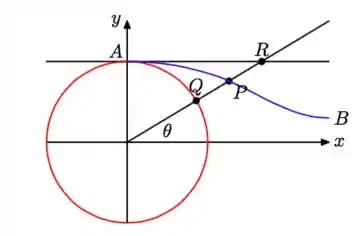
A reta que passa pela origem e faz ângulo com o eixo , intercepta a circunferência no ponto . Seja o ponto médio do segmento na figura abaixo. Determine as coordenadas de em função do ângulo . Perceba que, quando varia entre e , o ponto percorre a curva da figura.
Questão 2
Uma haste, presa na origem do plano , ocupa a posição da reta . A haste intercepta a reta no ponto e a elipse no ponto (figura). Quando varia, o vértice do triângulo descreve uma curva.
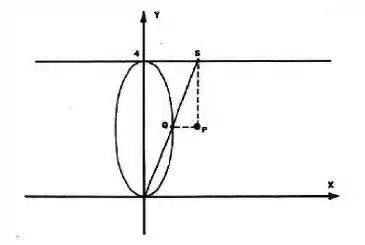
Escreva as equações paramétricas dessa curva em função do parâmetro .
Ver solução completaQuestão 3
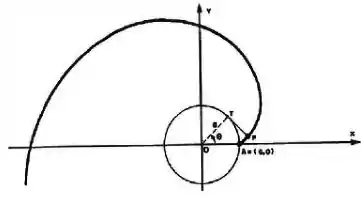
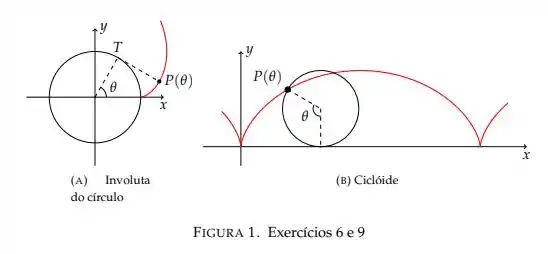
A involuta de uma circunferência é a curva traçada pelo ponto de extremidade de um fio quando o mesmo, mantido tenso, é desenrolado de um carretel fixo (figura). Supondo que o centro do carretel está colocado na origem do plano e seu raio é , e que o fio começa a se desenrolar no ponto . Mostre que as equações paramétricas da Involuta, ao desenrolar uma volta do fio no carretel são:
e ,
Utilizando como parâmetro o ângulo mostrado na figura.
Questão 4
Escreva equações vetorial e paramétricas para os planos:
b) que passa por
Ver solução completaQuestão 5
Obtenha equações do lugar geométrico (ou seja, para o conjunto) dos pontos médios dos segmentos com uma extremidade em e outra em e descreva-o geometricamente.
(a) e
Ver solução completaQuestão 6
Uma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
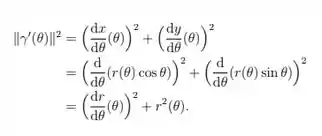
Assim o comprimento do arco da curva é dada pela equação:
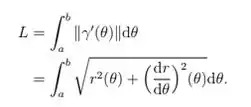
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaQuestão 7
Uma circunferência de raio rola sem escorregar ao longo do eixo . Encontre equações paramétricas para a curva descrita por um ponto da circunferência que se encontra inicialmente na origem. (Esta curva é chamada ciclóide, veja a Figura 1(b))
Questão 8
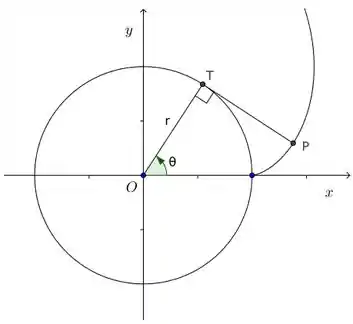
Um barbante é enrolado ao redor de um círculo, e então desenrolado sendo mantido esticado. A curva formada pelo ponto , no final do barbante, é chamada de involuta do círculo. Suponha que o círculo tem raio e centro , e que a posição final de seja . Se o parâmetro for escolhido como na figura, encontre as equações paramétrias da involuta.
Questão 9
Considere a curva , descrita pelo ponto , para , como na figura:
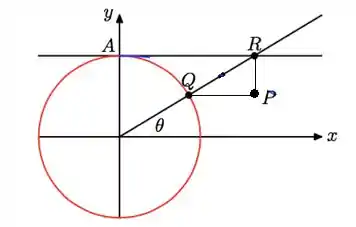
Onde o raio da circunferência é 1.
Uma parametrização de é:
- Nenhuma das demais alternativas.
Questão 10
Parametrize a curva C definida por
E esboce duas de suas projeções nos planos coordenados.
Ver solução completaQuestão 11
Dados o ponto e a reta , ache os pontos da reta r que distam do ponto A. A distância do ponto A à reta r é maior, menor ou igual a ? Por quê?
Ver solução completaQuestão 12
(Cap. 13.2 - Ex. 27) Encontre uma equação para a reta tangente à curva de intersecção dos cilindros e no ponto .
Ver solução completaQuestão 13
Obtenha uma equação geral do plano que contém e forma um ângulo de com o plano .
Ver solução completaQuestão 15
Obtenha equações da reta r que contém o ponto e é concorrente à reta , sabendo que o cosseno da medida angular entre r e s é igual a .
Ver solução completaQuestão 16
Uma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
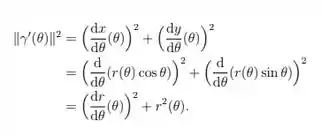
Assim o comprimento do arco da curva é dada pela equação:
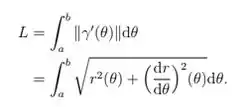
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaQuestão 17
Seja o campo vetorial . Seja a curva como a interseção do cilindro e o plano , orientada no sentido horário.
- Represente a integral de linha do campo vetorial sobre a curva através de uma integral simples definida.
- Determine o valor do campo vetorial sobre a curva .
Questão 18
Uma curva parametrizada em coordenadas polares é uma curva
onde da forma
Note que
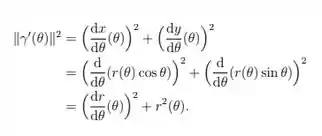
Assim o comprimento do arco da curva é dada pela equação:
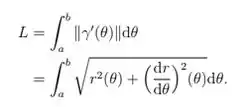
Usando isto, calcule o comprimento de arco quando da curva
Ver solução completaQuestão 25
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
- S é a parte da esfera interior ao cone ;
- S é a parte do cilindro compreendida entre os planos ;
- S é a parte do plano que é interior ao cilindro
- S é a parte parabolóide hiperbólico que está entre os cilindros
- S é a parte do cilindro que está no interior do cilindro , onde ;
- S é a parte da esfera que está no interior do cilindro , onde ;
- S é o toro obtido pela rotação da circunferência no plano com centro e raio em torno do eixo
- S é a parte da esfera com ;
- S é a parte do parabolóide limitada pela superfície ;
Questão 26
O plano contém A = (1, 0, 0), B = (0, 1, 0) e C = (0, 0, 1), o plano contém Q =
(−1, −1, 0) e é paralelo a ⃗u = (0, 1, −1) e ⃗v = (1, 0, 1), e o plano tem equação X = (1, 1, 1) +
λ(−2, 1, 0) + µ(1, 0, 1), λ, µ ∈ R.
(a) Obtenha uma equação geral para cada um dos três planos.
Ver solução completaQuestão 27
Dois pontos efetuam movimentos descritos pelas equações r : X = (0, 0, 0)Σ + λ(1, 2, 4) ,
λ ∈ R, e s : X = (1, 0, −2) + λ(1, 1, 1) , λ ∈ R. As trajetórias são concorrentes? Haverá colisão?
Ver solução completaQuestão 28
Escreva as equações paramétricas da reta que passa pelo ponto A = (2 , 0 , −3) e:
(a) é paralela à reta que passa pelos pontos B = (1 , 0 , 4) e C = (2 , 1 , 3).
(b) é paralela a
(c) é paralela à reta s :
Ver solução completaQuestão 29
Sendo o vetor um vetor normal ao plano que passa pelo ponto , escrever as equações paramétricas de .
Ver solução completaQuestão 30
O plano contém A = (1, 0, 0), B = (0, 1, 0) e C = (0, 0, 1), o plano contém Q =
(−1, −1, 0) e é paralelo a ⃗u = (0, 1, −1) e ⃗v = (1, 0, 1), e o plano tem equação X = (1, 1, 1) +
λ(−2, 1, 0) + µ(1, 0, 1), λ, µ ∈ R.
(b) Mostre que a interseção dos três planos se reduz a um único ponto. Qual é este ponto?
Ver solução completaQuestão 31
Dadas as retas r, s e t cujas equações são dadas por:
, ,
encontrar os valores de m ∈ R de modo que:
- as retas r e s sejam paralelas e não coincidentes;
Questão 32
Dadas as retas r, s e t cujas equações são dadas por:
, ,
encontrar os valores de m ∈ R de modo que:
c) as retas r e t sejam concorrentes;
Ver solução completaQuestão 33
Dadas as retas r, s e t cujas equações são dadas por:
, ,
encontrar os valores de m ∈ R de modo que:
d) as retas r e s sejam reversas.
Ver solução completaQuestão 34
Determine a projeção ortogonal do ponto P = (4, 0, 1) sobre o plano π : 3x − 4y + 2 = 0.
Ver solução completaQuestão 36
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
- S é a parte da esfera interior ao cone ;
- S é a parte do cilindro compreendida entre os planos ;
- S é a parte do plano que é interior ao cilindro
- S é a parte parabolóide hiperbólico que está entre os cilindros
- S é a parte do cilindro que está no interior do cilindro , onde ;
- S é a parte da esfera que está no interior do cilindro , onde ;
- S é o toro obtido pela rotação da circunferência no plano com centro e raio em torno do eixo
- S é a parte da esfera com ;
- S é a parte do parabolóide limitada pela superfície ;
Questão 37
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
- S é a parte da esfera interior ao cone ;
- S é a parte do cilindro compreendida entre os planos ;
- S é a parte do plano que é interior ao cilindro
- S é a parte parabolóide hiperbólico que está entre os cilindros
- S é a parte do cilindro que está no interior do cilindro , onde ;
- S é a parte da esfera que está no interior do cilindro , onde ;
- S é o toro obtido pela rotação da circunferência no plano com centro e raio em torno do eixo
- S é a parte da esfera com ;
- S é a parte do parabolóide limitada pela superfície ;
Questão 38
Determine uma representação paramétrica de cada uma das superfícies abaixo e calcule sua área:
- S é a parte da esfera interior ao cone ;
- S é a parte do cilindro compreendida entre os planos ;
- S é a parte do plano que é interior ao cilindro
- S é a parte parabolóide hiperbólico que está entre os cilindros
- S é a parte do cilindro que está no interior do cilindro , onde ;
- S é a parte da esfera que está no interior do cilindro , onde ;
- S é o toro obtido pela rotação da circunferência no plano com centro e raio em torno do eixo
- S é a parte da esfera com ;
- S é a parte do parabolóide limitada pela superfície ;