Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 55

A curva com a equação y 2 = x 2 x + 3 é chamada cúbica de Tschirnhausen. Se você colocar essa curva em um gráfico, verá que parte dela forma um laço. Encontre a área dentro desse laço.

Passo 1

O enunciado nos dá a seguinte curva:

y 2 = x 2 x + 3

O problema diz que o gráfico dessa curva tem o formato de laço e ele pede pra a gente encontrar o valor da área dentro desse laço!

Vamos esboçar a curva pra visualizamos melhor! Pra isso precisamos reescrever a função:

y = ± x 2 x + 3

y = ± x x + 3

Vamos calcular as raízes dessa função:

0 = ± x x + 3

x = 0

x = - 3

Esboçando a curva, temos:

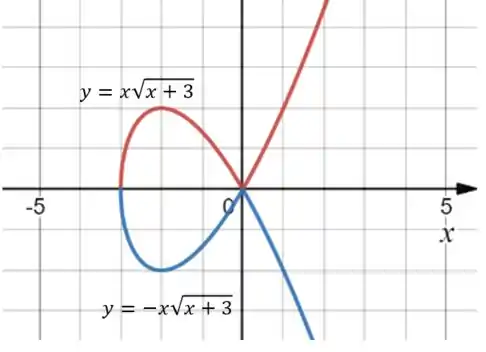
Passo 2

A área total é o dobro da área da curva acima do eixo x . Isso porque a área abaixo e acima do eixo x tem o mesmo valor, mas a de cima é negativa e a de baixo é positiva!

2 ∫ - 3 0 x x + 3   d x

Agora vamos calcular essa integral usando a substituição:

u = x + 3

d u d x = 1 → d u = d x

2 ∫ - 3 0 x x + 3   d x = 2 ∫ - 3 0 u - 3 u   d u

Temos que:

2 ∫ - 3 0 u - 3 u   d u = 2 ∫ - 3 0 u u - 3 u   d u

2 ∫ - 3 0 u 3 2 - 3 u 1 2   d u

Agora sim, integramos:

2 ∫ - 3 0 u 3 2 - 3 u 1 2   d u = 2 u 5 / 2 5 / 2 - 3 u 3 / 2 3 / 2 - 3 0

Aplicando os limites de integração:

A = - 2 2 5 x + 3 5 2 - 2 x + 3 3 2 0 3

A = 24 5 3

Prontinho!

Resposta

A = 24 5 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.79. x = y 2 - 1ex = | y | 1 - y ² ²
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.77. x + y 2 = 0ex + 3 y 2 = 2
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 73-80.76. x - y 2 = 0ex + 2 y 2 = 3
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 63-72.69. y = x 4 - 4 x 2 + 4ey = x ² ²
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 63-72.71. y = | x |e5 y = x + 6 Quantos pontos de intersecção existem?