Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 5.6 - Ex. 71
Determine as áreas das regiões compreendidas entre as retas e as curvas nos Exercícios 63-72.
71.
Quantos pontos de intersecção existem?
Passo 1
Inicialmente, o que precisamos fazer é plotar esses gráficos para determinarmos as regiões compreendidas entre eles, ok? Se plotarmos os gráficos, teremos:
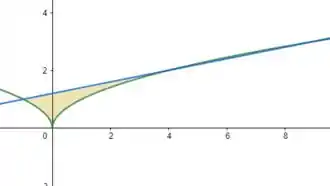
No qual a função em verde é e a função em azul é . Uma vez plotados, o que precisamos descobrir é a área dessas rachuras aí, certo? Aqui vale um comentário: não dá para enxergar direito na figura, mas há uma área rachurada entre 4 e 9, e isso é extremamente importante para nossa resolução! Para descobrirmos a área dessas rachuras temos que descobrir os pontos em que as funções se encontram, e é aqui que surge um trabalho mais sério, se liga!
Passo 2
Temos que descobrir os pontos em que as funções se encontram para sabermos quais serão os limites de integração da nossa integral, galera! Para descobrirmos, basta igualarmos as duas funções! No entanto, uma das funções é modular, então essa função admite as seguintes soluções:
Utilizando a restrição para primeiro, teremos:
Descobrindo as raízes dessa função, teremos:
No entanto, como podemos notar no gráfico, não é solução dessa equação! Sendo assim, podemos escrever nossa equação para da seguinte forma:
Passo 3
Agora utilizando a restrição para , teremos:
Descobrindo as raízes dessa função, teremos:
Dessa forma, podemos escrever nossa equação para da seguinte maneira:
Sendo assim, assim como podemos notar na figura do passo 1, teremos que descobrir o valor de 3 integrais, cujo intervalo de integração para essas integrais acabamos de descobrir!
Passo 4
Para calcularmos a área de uma região, assim como discutido na seção 6 do George, o que precisamos descobrir é quais são as curvas superiores e inferiores. Depois de descoberto isso, basta fazermos:
Onde, nesse caso, seria a curva superior e seria a curva inferior.
Para a primeira região rachurada da figura do passo 1, a curva superior é e a curva inferior é . Ademais, o intervalo é: .
Para a segunda região rachurada da figura do passo 1, a curva superior é e a curva inferior é . Ademais, o intervalo é: .
Para a terceira região rachurada da figura do passo 1, a curva superior é e a curva inferior é .
Passo 5
Agora que já temos TUUUDO que precisamos, basta escrevermos as integrais, se liga:
Como já resolvemos essa integral anteriormente, então:
Lembrando que para resolvermos todas essas integrais, a única regra que utilizamos foi:
Passo 6
Agora que encontramos todas as “parcelas” de área, temos que a área total é a soma de todas essas áreas que encontramos. Dessa forma, teremos: