Curva de Maria Agnesi - A curva em formato de sino de Maria Agnesi pode ser feita da seguinte forma: inicie com um círculo de raio 1, centrado no ponto , conforme exibido na figura a seguir. Escolha um ponto A na reta e conecte-o à origem com um segmento de reta. Designe por B o ponto onde o segmento cruza o círculo. Seja P o ponto em que a reta vertical por A cruza a reta horizontal que passa por B. A curva de Agnesi é a curva traçada por P conforme A se move ao longo da reta . Encontre equações paramétricas e um intervalo paramétrico para a curva de Agnesi expressando as coordenadas de em termos de , a medida em radianos do ângulo que o segmento faz com o eixo positivo. As seguintes igualdades (que você pode assumir) irão ajudar
a.
b.
c.
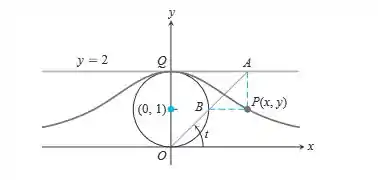
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
Primeiramente, vamos considerar o triângulo , nós podemos escrever que
Vamos considerar que , porque eles são ângulos internos alternados, logo
Isolando o ,
Passo 2
Agora, com essas informações, já podemos escrever que
E com isso
Portanto, o arco é igual a
É fornecido que
Substituindo e
E então, é igual a
Passo 3
Substituindo o valor de em
Simplificando os termos, nós temos que
Pela figura, nós podemos ver o seguinte intervalo .