Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.3 - Ex. 21
Desenhe os gráficos dos conjuntos de pontos cujas coordenadas polares satisfaçam as equações e desigualdades nos Exercícios 11-26.
Passo 1
Olá pessoal, espero que todos estejam bem e animados para este exercício. Vamos lá!
Se mantivermos fixo em um valor constante , o ponto estará a unidades a partir da origem . Conforme varia em qualquer intervalo de comprimento , traça um círculo de raio centrado em , de acordo com a Figura:
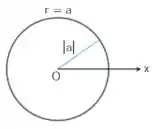
Se mantivermos fixo em um valor constante e fizermos variar entre e , o ponto traça a reta que passa por , que forma um ângulo de medida com o raio inicial.
Além disso, sabemos que o círculo trigonométrico em radianos é:
Passo 2
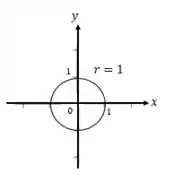
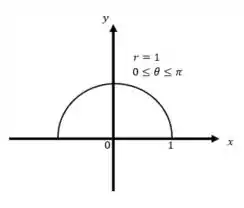
Primeiramente iremos desenhar a Figura para :
E o ângulo no intervalo :
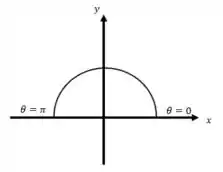
Sendo assim, a Figura que satisfaz as nossas condições é definida por:
Tchau pessoal.
Resposta
Resposta no Passo 2.