O custo, em dólares, da produção de x jardas de um certo tecido é C x = 1200 + 12 x - 0,1 x 2 + 0,0005 x 3 e a companhia descobre que se vender as x jardas ela poderá cobrar p x = 29 - 0,00021 x dólares por jarda do tecido.Faça o gráfico das funções custo e rendimento e use-os para estimar o nível da produção para o lucro máximo.

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.8 - Ex. 17a

O custo, em dólares, da produção de jardas de um certo tecido é e a companhia descobre que se vender as jardas ela poderá cobrar dólares por jarda do tecido.

Faça o gráfico das funções custo e rendimento e use-os para estimar o nível da produção para o lucro máximo.

Passo 1

Primeiro vamos representar as funções do custo e do rendimento. O custo é dado, e podemos calcular o rendimento multiplicando o preço por jarda pelo número de jardas:

Agora usamos um programa para traçar os dois gráficos:

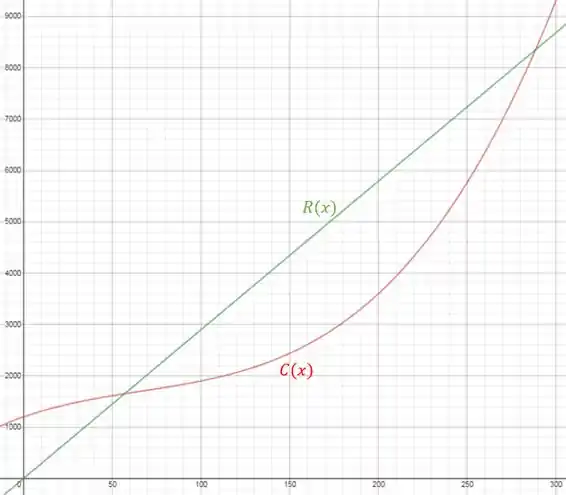
Passo 2

O lucro é o rendimento menos o custo. Para que o lucro seja maximizado, a sua derivada deve ser nula. Então:

Se as derivadas do rendimento e do custo são iguais, no valor para o qual o lucro é máximo as retas tangentes às curvas de e devem ter a mesma inclinação, ou seja, devem ser paralelas. Além disso, deve ocorrer na região na qual o rendimento é maior que o custo (senão temos um prejuízo e não lucro!). Pelo gráfico, podemos tentar estimar o valor de para o qual isso acontece:

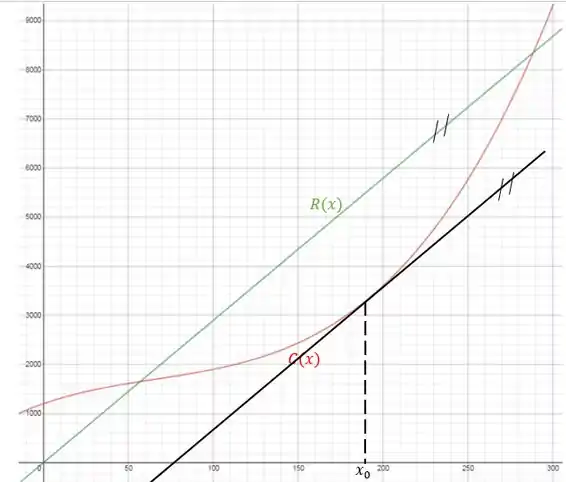
Como podemos ver, isso ocorre para aproximadamente igual a 190.

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

10 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De

12 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De

13. O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. D

11. O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. D

14 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde s cm é a distância da partícula a partir de um pontoO , em t s. A direção positiva é à direita. De