Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.9 - Ex. 28
Use o método de Newton para encontrar todas as raízes da equação corretas até a oitava casa decimal. Comece fazendo um gráfico para encontrar a primeira aproximação inicial.
Passo 1
Fala aí, eu sou o Rafha do Responde Aí e vou te ajudar aqui.
Nessa questão temos a seguinte equação:
E queremos encontrar todas as raízes da equação com precisão de seis casas decimais.
Para isso vamos usar um método iterativo que é o método de Newton.
O método de Newton encontra as raízes de uma função de forma que:
Reescrevendo nossa equação encontramos a função que queremos achar as raízes:
Logo,
No método de Newton, basicamente, nós começamos com um chute inicial para essa raiz.
E para encontrar o próximo valor, faremos a seguinte iteração:
O enunciado pede para encontrarmos a raíz com uma precisão de oito casas decimais. Bora lá?
Passo 2
Queremos encontrar as raízes da função:
Usando o método de Newton, as aproximações são dadas pela fórmula:
Temos:
Sua derivada é portanto:
Então a fórmula fica:
Agora basta escolher uma aproximação inicial adequada, e então aplicar a fórmula até os resultados não diferirem na sexta casa decimal.
Passo 3
Para escolher o valor inicial olhamos um esboço das funções e .
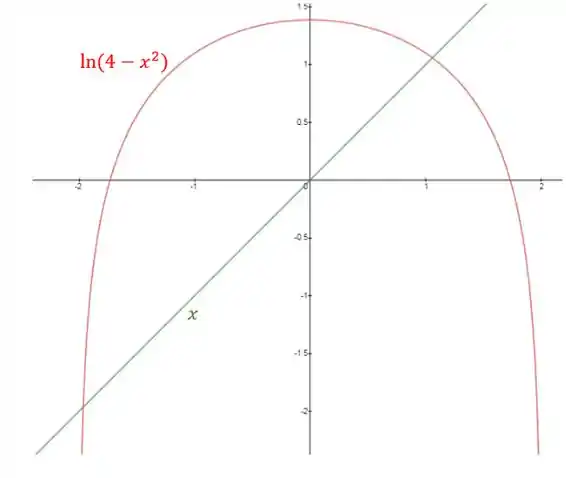
Os pontos onde esses gráficos se interceptam são pontos onde:
Que são as raízes que estamos procurando.
Temos duas raízes, ummuito próxima de -2 e uma muito próxima de 1. Usaremos para a primeira raiz uma aproximação , e para o segundo . Não usamos o valor -2 pois a derivada não existe pra esse valor.
Passo 4
Vamos calcular a primeira raiz.
Calculamos as próximas aproximações (vai vir um paredão de conta agora, mas não se assuste o procedimento é sempre o mesmo, use o paredão a seguir apenas para verificar se suas contas estão certas):
Como e não diferem até a oitava casa decimal:
Passo 5
Fazemos o mesmo procedimento para achar a outra raiz:
Como e não diferem até a oitava casa decimal: