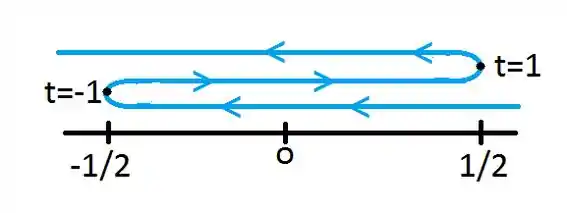
12 O movimento de uma partícula é ao longo de uma reta horizontal, de acordo com a equação dada, onde cm é a distância da partícula a partir de um ponto, em s. A direção positiva é à direita. Determine os intervalos de tempo em que a partícula move-se para a direita e para a esquerda. Determine também quando a partícula reverte o sentido do movimento. Mostre o comportamento do movimento através de uma figura similar à Figura 2 e escolha valores de ao acaso, mas inclua os valores de em que a partícula muda o sentido do movimento.
Passo 1
Para que alguma coisa que está se mexendo pra direita mude de direção e vá para a esquerda é necessário que em algum momento ela pare de se mexer, isso acontece exatamente quando a velocidade é zero, pois a velocidade de uma coisa parada é zero, além disso o sentido da velocidade indica o sentido do movimento. Como já foi abordado nos exercícios anteriores .
Então bora derivar!
Passo 2
Pra derivar essa função eu escolhi fazer por regra do quociente:
Passo 3
Agora precisamos dos valores de onde a partícula para de se mover, olhando pra o denominador de sabemos que ele será sempre positivo pois esta ao quadrado, a única coisa que pode mudar o valor de será seu numerador.
Passo 4
Para estudarmos o sinal de usaremos métodos sofisticados do nono ano, o sinal de será dado dada por uma parábola de com cavidade pra baixo e com raízes 1 e -1.
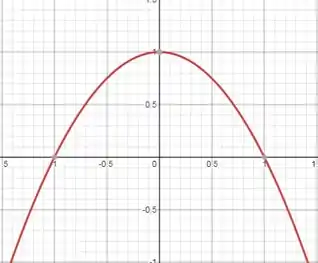
Passo 5
Chegou a hora de montar o gráfica e ver que beleza ficou, pra isso vamos precisar dos valores de onde a partícula muda de sentido, mas relaxa é só substituir e em .
Resposta