Exercícios de Otimização - Lista de Exercícios Resolvida
Questão 1
A altura de um corpo que se desloca verticalmente é dada por:
Com em metros e em segundos. Determine a altura máxima do corpo.
Ver solução completaQuestão 2
Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionado com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Ver solução completaQuestão 3
Q1. Considere todos os retângulos que possuem base contida no segmento que une os pontos e e os vértices opostos pertencentes à parábola
a) Dentre todos esses retângulos, determine o comprimento da base que possui maior área.
b) Mostre que, dentre todos esses retângulos, existem um, e apenas um, que possui diagonal medindo . Justifiqur cuidadosamente sua resposta.
Ver solução completaQuestão 4
Encontre o ponto sobre a curva (onde ) que está mais próximo do ponto .
Ver solução completaQuestão 5
Considere a função definida por . Considere a função tal que é a inclinação da reta tangente ao gráfico de no ponto . Determine o valor máximo e o valor mínimo da função .
Ver solução completaQuestão 6
5. Determine as dimensões de um retângulo com perímetro cuja a área seja a maior possível. Justifique com detalhes!
Ver solução completaQuestão 7
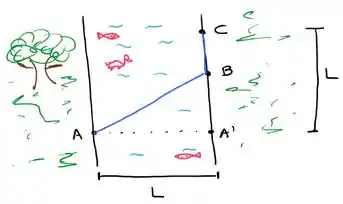
Uma pessoa no ponto da margem de um rio tem que atravessá-lo para chegar ao ponto da margem oposta (vide figura abaixo). A largura do rio é e a distância ao longo do rio entre os pontos (obtido atravessando o rio perpendicularmente à sua margem) e também é .
A figura abaixo mostra um possível caminho para isso, onde a pessoa sai do rio no ponto .
A velocidade da pessoa em terra é e na água é . Você pode, se quiser, trabalhar nas unidades em que e . Determine a distância de a para que o tempo gasto seja mínimo.
Questão 8
Se de um material estiver disponível para fazer uma caixa com uma base quadrada e sem tampa. Encontre o maior volume possível para a caixa.
Ver solução completaQuestão 9
Você planeja fechar um canto do primeiro quadrante com um segmento de reta de 20 unidade de comprimento, que vai de (a, 0) a (0, b). Mostre que a área do triângulo determinada pelo segmento é máxima quando a = b.
Ver solução completaQuestão 10
Um projétil é lançado verticalmente para cima e segundos após o lançamento está a metros do solo, onde. Calcule:
(a) A velocidade do projétil segundos após o lançamento;
(b) O tempo necessário para o projétil atingir a altura máxima;
(c) A altura máxima atingida pelo projétil.
Ver solução completaQuestão 11
Ache as dimensões do maior jardim retangular que pode ser fechado com 100 de cerca.
Ver solução completaQuestão 12
Um fabricante de latas cilíndricas de conservas recebe um pedido muito grande de latas com determinado volume . Quais as dimensões que minimizarão a área total da superfície de uma lata como esta, e, portanto, de metal necessário para fabricá-la?
Ver solução completaQuestão 13
Um empresário deseja abrir uma pequena fábrica. Segundo um estudo feito por ele, se funcionários forem contratados, seu lucro anual em reais será de
O estudo considera a possibilidade de contratar até 80 funcionários. Quantos funcionários devem ser contratados para que o lucro anual seja o maior possível? E qual o valor desse lucro?
Ver solução completaQuestão 14
Achar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completaQuestão 15
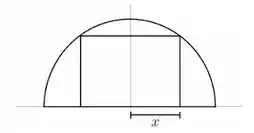
- Determine o domínio e a expressão da função que fornece a área do retângulo em termos da variável .
- Determine a área do retângulo de maior área possível que pode ser escrito em uma semicircunferência de raio e cento na origem.
Questão 16
Ache as dimensões do maior jardim retangular que pode ser fechado com 100 de cerca.
Ver solução completaQuestão 17
Uma ilha situada a da costa deve ter um serviço de barcos para uma cidade A (figura ao abaixo). Se os barcos têm velocidade média de e os carros uma velocidade média de , onde deverá estar situada a estação de barcos na costa, a fim de tornar a via a mais rápida possível?

Questão 18
Constrói-se uma janela normanda colocando-se um semicírculo em cima de uma janela retangular. Encontre as dimensões da janela de área máxima, sabendo-se que seu perímetro é de .
Ver solução completaQuestão 19
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.
Ver solução completaQuestão 20
Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionado com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Ver solução completaQuestão 21
É preciso delimitar um terreno que tenha formato retangular de usando muros externos e divisórias internas como na figura.

Sabendo-se que o preço do muro é e o preço das divisórias é , determine as dimensões do terreno de modo que o custo total seja o menor possível.
Ver solução completaQuestão 22
Questão 2:
Considere um triângulo com um vértice no ponto e outros dois vértice, e , pertencentes à curva de equação . As seguintes condições devem ser satisfeitas:
- O lado é paralelo ao eixo .
- A abscissa (coordenada ) do vértice é maior que as abscissas dos vértices e .
- A ordenada (coordenada ) do vértice é maior que a ordenada do vértice .
Seja a abscissa do vértice .
- Determine o domínio e a expressão da função que fornece a área do triângulo em termos de .
- Determine a área do triângulo que tem área máxima.
Obs.: Respostas sem justificativas não serão aceitas.
Ver solução completaQuestão 23
Questão 1) Determinar o ponto da curva , com , mais próximo da origem do sistema de coordenadas.
Ver solução completaQuestão 24
Determine a altura do cone circular reto, de volume máximo, e com a geratriz dada.
Ver solução completaQuestão 25
Uma caixa com uma base quadrada e sem tampa tem um volume de Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Ver solução completaQuestão 26
Jurema tem uma folha de cartolina retangular com dimensões . Ela gostaria de fazer uma caixa sem tampa cortando quadrados iguais nos quatro cantos da folha e dobrando para cima os quatro lados. Determine as dimensões da caixa que Jurema pode fazer de modo que seu volume seja máximo.
Ver solução completaQuestão 27
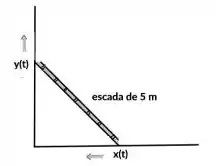
Uma escada de de comprimento está apoiada em uma parede vertical. A base da escada, que está ́a apoiada no chão, está a sendo empurrada na direção da parede a uma
velocidade constante de . Com que velocidade o topo da escada sobe quando a base da escada está da parede?
Questão 28
Uma cerca de de altura está situada a uma distância de da parede lateral de um galpão. Qual o comprimento da menor escada cujas extremidades se apoiam na parede e no chão do lado de fora da cerca?
Ver solução completaQuestão 29
Uma caixa com uma base quadrada e sem tampa tem um volume de . Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Ver solução completaQuestão 30
4. Um determinado produto tem um preço de custo de por unidade, e ao vender o produto por , é possível vender . Além disso, a cada centavo descontado no preço, é possivel aumentar a venda em . Reciprocamente, ao aumentarmos em um centavo o preço de venda, deixamos de vender . Que preço deve ser cobrado no produto, para que o lucro obtido seja máximo?
Ver solução completaQuestão 31
Uma refinaria de petróleo está em A na margem norte de um rio reto que tem de largura. Um oleoduto deve ser construído da refinaria até um tanque de armazenamento em B na margem sul do rio, a leste da refinaria. O custo de construção do oleoduto é sobre a terra, até um ponto P na margem norte do rio e sob o rio até o tanque.
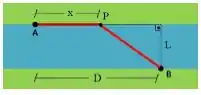
- Obtenha o custo total de construção do oleoduto, , em função da distância , entre A e P.
- Determine os pontos críticos de em .
- Qual o valor de que minimiza o custo de construção do oleoduto?
Questão 33
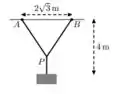
- Um peso deve ficar suspenso a 4m de uma superfície horizontal por meio de uma armação de arame em forma de Y, como na figura abaixo (os pontos A, B e P são os vértices de um triângulo isósceles). Se os pontos de sustentação A e B distam m, determine o comprimento mínimo de arame necessário.
Questão 34
- Uma peça mecânica é construída a partir de uma esfera de raio R na qual faz-se um pequeno furo cilíndrico cujo eixo de simetria passa exatamente pelo centro da esfera. Determine o raio do furo para o qual a área total seja máxima.
Ver solução completaQuestão 35
Encontre o ponto sobre a curva (onde ) que está mais próximo do ponto .
Ver solução completaQuestão 36
Uma escada de está encostada em uma parede. Se a extremidade inferior da escada for afastada do pé da parede a uma velocidade constante de , com que velocidade a extremidade superior estará descendo no instante em que a inferior estiver a da parede?
Ver solução completaQuestão 37
O comprimento de um retângulo está aumentando a uma taxa de e sua largura está aumentando a uma taxa de . Quando o comprimento for e a largura for quão rápido a área do retângulo está aumentando?
Ver solução completaQuestão 38
7. Um hortigranjeiro quer construir um galinheiro retangular de área máxima. Em sua propriedade dispõe de cento e vinte metros de tela. Como construir de modo otimizado?
Ver solução completaQuestão 39
5) No instante , a posição do corpo que se desloca ao longo do eixo é metros.
a) Determine os valores de onde a velocidade é zero.
b) Determine os valores da aceleração onde a velocidade é zero.
Ver solução completaQuestão 40
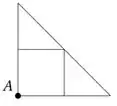
Considere retângulos inscritos em um triângulo retângulo com os dois lados do retângulo sobre os catetos do triângulo e o vértice A em comum. Determine as medidas do retângulo de maior área que pode ser inscrito em um triângulo retângulo com catetos de comprimentos 3 cm e 4 cm. Qual a área do retângulo encontrado? (Dica: use semelhança de triângulos para montar a função a ser otimizada).
Questão 41
Uma tela de cinema de de altura está fixado numa parede, com sua base 4 m acima de seus olhos conforme a figura abaixo.
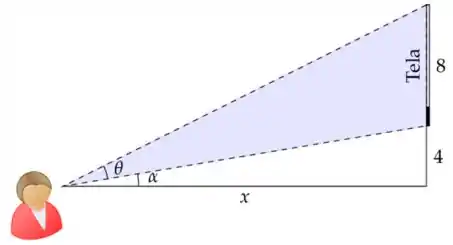
Se é a distância a que você deve ficar da parede para que seu ângulo de visão da tela seja máximo, então vale:
Ver solução completaQuestão 42
Seja T um triângulo de base B e altura H cujas ângulos internos em relação à base são agudos. Mostre que dentre todos os retângulos que podem ser inscritos nesse triângulo, o de maior volume tem base b = B/2 e altura h = H/2.
Ver solução completaQuestão 43
Escreva o número 8 como soma de dois números reais positivos de tal modo que a soma do quadrado do primeiro com o cubo do segundo seja mínima. É possível fazer essa decomposição de modo que a soma seja máxima?
Ver solução completaQuestão 44
Determine uma reta tangente ao gráfico de de modo que a distância da origem até seja a menor possível.
Ver solução completaQuestão 45
Uma lata cilíndrica sem topo é feita para receber de líquido. Encontre as dimensões que minimizarão o custo do metal usado para fazer a lata.
Ver solução completaQuestão 46
Achar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completaQuestão 47
Determine o número real positivo cuja soma com o inverso de seu quadrado seja mínima.
Ver solução completaQuestão 48
Duas partículas e movem-se, respectivamente, sobre os eixos e . A função de posição de é e a de , , . Determine o instante em que a distância entre e seja a menor possível.
Ver solução completaQuestão 49
Deseja-se construir um prédio em forma prisma retangular reto de modo a minimizar as perdas de calor pela superfície do prédio. As fachadas norte e sul perdem calor a uma taxa de por dia; as fachadas leste e oeste perdem por dia a cada dia; já o piso e o teto perdem calor a uma taxa de por dia. Suponha que o volume do prédio deve ser de , que cada fachada deve ter ao menos de comprimento e que a altura do prédio deve ser de no mínimo .
a) Determine e esboce o domínio da função que descreve a perda de calor por dia em
função do comprimento e largura do prédio.
b) Encontre as dimensões que minimizem a perda de calor por dia.
c) Seria possível, removendo a restrição sobre a altura do prédio, projetar um prédio
que tenha menor perda de calor? Justifique.
Ver solução completaQuestão 50
8. Um hortigranjeiro quer construir um galinheiro retangular de área máxima. Em sua propriedade ele dispõe de um muro de 80 metros que pode ser usado como um dos lados do galinheiro. Além disso, ele possui cento e oitenta metros de tela. Como construir de modo otimizado?
Ver solução completaQuestão 51
9. Deseja construir um celeiro em um terreno retangular de área igual à . Sendo um lado do muro já levantado, quais as medidas desse celeiro para que o muro tenha o menor comprimento possível.
Ver solução completaQuestão 52
10. Uma lata cilíndrica fechada deve conter 1 litro de líquido. Como poderíamos escolher a altura e o raio para minimizar a quantidade de material usado na confecção da lata?
Ver solução completaQuestão 53
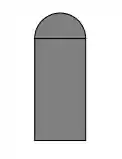
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. Se o perímetro da janela for , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.
Questão 54
Um fabricante produz por semana toneladas de um certo produto. O preço de venda é de unidades monetárias por tonelada do produto e está relacionada com por , . O custo de produção é de unidades monetárias. Determine para que o lucro seja máximo. Determine, também, o lucro máximo.
Ver solução completaQuestão 55
Entre todas as latas cilíndricas de volume 1 litro, raio da base e altura , qual a que tem menor área superficial.
Ver solução completaQuestão 56
Suponha que ao completar anos, , a massa aproximada de um animal seja dada em quilos pela expressão
Sabendo que pretende-se sacrificar o animal no momento em que este possuir a maior massa, determine com qual idade o animal deve ser abatido.
Ver solução completaQuestão 57
Supondo que o lucro, em milhões de reais, obtido na venda de x nmil unidades de um produto é dado por:
Determine a quantidade de itens que devem ser vendidos de modo a maximizar o lucro.
Ver solução completaQuestão 58
Uma cerca de de altura está situada a uma distância de da parede lateral de um galpão. Qual o comprimento da menor escada cujas extremidades se apoiam na parede e no chão do lado de fora da cerca?
Ver solução completaQuestão 59
Com que dimensões uma caixa com base quadrada e sem tampa pode ser construída de forma que seu volume seja máximo, utilizando-se de 1200cm² de papelão?
Ver solução completaQuestão 61
Considere a reta de equação .
Indique uma fórmula para a distância à origem de um ponto da reta, em função da abcissa só.
Calcule o ponto que minimiza essa distância.
Quanto vale essa distância mínima?
(Obs: minimizar a distância é equivalente a minimizar o quadrado da distância).
Ver solução completaQuestão 62
Uma partícula move-se de acordo com os dados a seguir,
,
onde indica a velocidade e indica a posição. A posição da partícula no tempo é (escolha):
Ver solução completaQuestão 63
Um fabricante de um determinado produto sabe que se produtos forem produzidos, cada um poderá ser vendido por reais. Sabe-se que o custo de produção de produtos é de . Quantos produtos o fabricante deve produzir para obter um lucro máximo e qual será o valor desse lucro?
Ver solução completaQuestão 64
Mostre que dentre todos os retângulos com o mesmo perímetro, aquele com a maior área é um quadrado.
Ver solução completaQuestão 65
Um galpão deve ser construído com uma área retangular de . E necessário que haja um recuo de 25 m na frente, 15 m na parte traseira e 5 m em cada lado. Encontre as dimensões do lote de área mínima na qual tal galpão pode ser construído. Faça um esboço da situação.
Ver solução completaQuestão 66
Determine os pontos sobre a parábola que estão mais próximos e distantes do ponto para . Qual é a menor distância? E a maior distância? Faça um desenho representando todos os pontos envolvidos.
Ver solução completaQuestão 67
Ao preço de R$ 1,50, um vendedor pode vender 500 unidades de uma certa mercadoria que custa R$ 0,70 cada. Para cada centavo que o vendedor abaixa no preço, a quantidade vendida aumenta em 25 unidades. Que preço de venda maximizaria o lucro?
Ver solução completaQuestão 69
Uma lata cilíndrica deve ser produzida com volume igual a O custo do material da tampa e da base da lata é de centavos por , enquanto o custo do material da parte lateral é de centavos por . Quais devem ser as dimensões da lata de forma a minimizar os custos?
Ver solução completaQuestão 70
Qual é o paralelepípedo retangular de base quadrada e volume que tem a menor área total?
Ver solução completaQuestão 71
Encontre a área do maior retângulo que pode ser inscrito em um semicírculo de raio r.
Ver solução completaQuestão 72
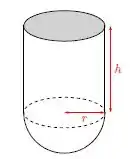
Um sólido será construído acoplando-se a um cilindro circular reto, de altura e raio , uma semiesfera de raio . Deseja-se que a área da superfície do sólido seja . Determine e para que o volume seja máximo.
Questão 73
Um empresário deseja abrir uma pequena fábrica. Segundo um estudo feito por ele, se funcionários forem contratados, seu lucro anual em reais será de
O estudo considera a possibilidade de contratar até 80 funcionários. Quantos funcionários devem ser contratados para que o lucro anual seja o maior possível? E qual o valor desse lucro?
Ver solução completaQuestão 74
Dois produtos e , são produzidos por determinada fábrica. Se for o custo total de produção numa jornada de 8 horas por dia, então , onde e são o número de máquinas que são usadas para produzir e , respectivamente. Se durante a jornada de horas tivermos máquinas em funcionamento, determine quantas devem produzir e quantas devem produzir , para que o custo total seja mínimo.
Ver solução completaQuestão 75
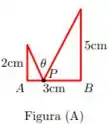
Como deve ser escolhido o ponto P na figura (A) abaixo de modo que o ângulo seja máximo?
Questão 76
A área entre dois círculos concêntricos variáveis �� constante igual a . A taxa de variação da área do círculo maior é de . Qual a taxa de variação do raio em relação ao tempo do círculo menor quando ele tem área ?
Ver solução completaQuestão 77
Um objeto circular tem seu raio variando de maneira desconhecida, mas sabe-se que quando seu raio e , a taxa de variação deste e . Determine a taxa de variação da área do objeto no instante em que seu raio e .
Ver solução completaQuestão 78
Suponha agora que o objeto circular do exercício anterior e, na verdade, um equador de um objeto esférico. Determine a taxa de variação do volume do objeto e de sua área, quando o raio é .
Ver solução completaQuestão 79
A partícula A se move ao longo do semieixo positivo e a partícula B move-se ao longo do gráfico da função . Num certo instante, a partícula A está no ponto (5, 0) e afasta-se da origem com velocidade unidades por segundo e a distância de B até a origem e unidades, afastando-se da origem com velocidade unidades por segundo. Qual a taxa de variação da distância entre A e B nesse instante?
Ver solução completaQuestão 80
Num certo instante , a altura de um triangulo cresce a razão e sua área aumenta a razão de . No instante , sabendo que sua altura a e sua área e , qual a taxa de variação em relação ao tempo da base do triangulo?
Ver solução completaQuestão 81
Despeja-se areia sobre o chão fazendo um monte que tem, a cada instante, a forma de um cone com diâmetro da base igual a três vezes a altura. Quando a altura do monte e de , a taxa de variação com que a areia e despejada e de . Qual a taxa de variação da altura do monte neste instante?
Ver solução completaQuestão 82
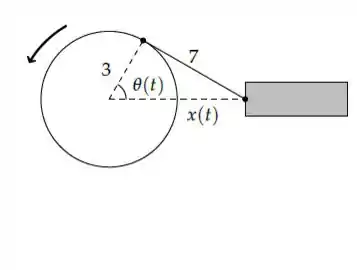
Num motor a combustão, uma biela de tem uma de suas extremidades acoplada a uma manivela cujo raio é de . Na outra extremidade da biela está um pistão que se move quando a manivela gira (vide Figura abaixo). Sabendo que a manivela gira no sentido anti-horário a uma taxa constante de rotações por minuto, calcule a velocidade do pistão quando o ângulo de rotação do disco é (medido a partir da posição em que o pistão está mais afastado do disco).
Questão 83
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
- Qual a velocidade com a qual o topo da escada se move nesse instante?
Questão 84
Uma lâmpada esta acesa no solo a de um edifício. Um homem de de altura anda a partir da luz em direção ao edifício a . Determine a velocidade com que o comprimento de sua sombra sobre o edifício diminui quando ele está a do edifício e quando ele está a do edifício.
Ver solução completaQuestão 85
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
b) Considere o triângulo formado pela parede da casa, a escada e o chão. Calcule a taxa de variação da área deste triangulo no instante em que a base da escada se encontra a da parede.
Ver solução completaQuestão 86
Uma escada de bombeiro com está encostada na parede de um prédio e sua base se afasta da parede. Num certo instante, a base da escada se encontra a da parede e sua velocidade é de .
c) Calcule a taxa de variação do ângulo formado entre a parede da casa e a escada, quando a base da escada estiver a da parede.
Ver solução completaQuestão 87
Uma câmera colocada no solo está filmando um ônibus espacial que está subindo verticalmente de acordo com a equação , sendo s a altura e t o tempo. A câmera está a 600 m do local de lançamento. Calcule a taxa de variação da distância entre a câmera e a base do ônibus espacial no instante t = 10 segundos após o lançamento (suponha que a câmera e a base do ônibus estão no mesmo nível no instante inicial t = 0).
Ver solução completaQuestão 88
Enche-se de água um reservatório a uma taxa de . O reservatório tem a forma de um
cone circular reto com vértice virado para baixo. O raio da base do cone é de e sua altura
é de . Com que velocidade o nível da água está subindo no instante em que ?
Ver solução completaQuestão 89
O comprimento de um retângulo está aumentando a uma taxa de 8 cm/s e sua largura está
aumentando a uma taxa de 3 cm/s. Quando o comprimento está 20 cm e largura está 10 cm,
quão rápido a área do retângulo está aumentando?
Ver solução completaQuestão 90
Uma empresa foi fundada em 1990 e sua capacidade de produção P = P (t) evoluiu segundo:
- Em que ano a empresa alcançou sua capacidade máxima de produção?
Questão 91
Encontre a área do maior retângulo que pode ser inscrito em um semi-cı́rculo de raio r.
Ver solução completaQuestão 92
Um cartaz deve conter 50 de matéria impressa com duas margens de 4 cm cada, na parte superior e na parte inferior e duas margens laterais de 2 cm cada. Determine as dimensões externas do cartaz de modo que sua área total seja mínima.
Ver solução completaQuestão 93
11. Uma caixa com uma base quadrada e sem tampa tem volume de . Encontre as dimensões da caixa que minimizam a quantidade de material usado.
Ver solução completaQuestão 94
Uma caixa fechada com base quadrada vai ter um volume de 2000 cm³ . O material da tampa
e da base vai custar R$3, 00 por centímetro quadrado e o material para os lados R$1, 50 por
centímetro quadrado. Encontre as dimensões da caixa de modo que o custo seja mínimo.
Ver solução completaQuestão 95
Considere dois números reais positivos tais que
Queremos minimizar a quantidade . Para isso:
- Determine uma função de uma variável tal que o valor mínimo de corresponda à solução do problema acima. Indique também o domínio dessa função.
- Determine o valor mínimo de , justificando sua resposta.
Questão 97
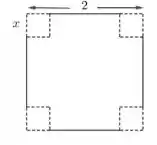
Uma caixa é feita retirando-se quatro quadrados dos cantos de uma folha de papel quadrada de lado e dobrando os lados, como na figura. O tamanho dos lados dos quadrados retirados para que o volume da caixa seja máximo pertence ao intervalo:
Questão 98
Uma luz está acesa no topo de um poste de 50 pés de altura. Uma bola cai da mesma altura em um ponto situado a 30 pés de distância do poste (Veja a figura a seguir). A que velocidade a sombra da bola se desloca no solo 1/2 segundo depois? (Considere que na queda a bola percorreu s = 16t 2 pés em t segundos)
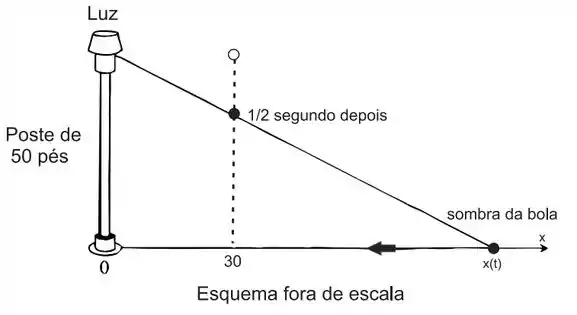
Questão 99
Latas cilíndricas fechadas devem ser feitas com um volume especificado. Qual é a razão entre a altura e o diâmetro da base que minimiza a quantidade de metal gasto para fazer a lata?
Por que as latas encontradas no mercado não são, em geral, como em Tipicamente, o metal é entregue em chapas retangulares. Não há desperdício envolvido em cortar a chapa que formará a superfície lateral, mas as tampas devem ser cortadas de uma peça quadrada e as sobreas são recicladas. Ache a razão entre a altura e o diâmetro de uma lata de volume que minimiza o custo do material utilizado.
Ver solução completaQuestão 100
Determine o cone circular reto de maior volume que pode ser inscrito numa esfera de raio .
Ver solução completaQuestão 101
Determinar a área da maior pastagem retangular que pode ser cercada fazendo 600 metros de cerca e utilizando 100 metros de cerca (reta) já existente.
Ver solução completaQuestão 102
9. Encontre as dimensões de um retângulo com perímetro de cuja área seja a maior possível.
Ver solução completaQuestão 103
12. Um contêiner para estocagem retangular com uma tampa aberta deve ter um volume de . O comprimento de sua base é o dobro da largura. O material para a base custa por metro quadrado. O materal para os lados custa por metro quadrado. Encontre o custo dos materiais para o mais barato desses contêineres.
Ver solução completaQuestão 104
10. Encontre as dimensões de um retângulo com área de cujo perímetro seja o menor possível
Ver solução completaQuestão 105
Dentre os cilindros circulares inscritos numa esfera de raio , seja a altura daquele que tem volume máximo e seja a altura daquele que tem superfície lateral máxima. Então, é:
Ver solução completaQuestão 106
Considere todos os triângulos retângulos formados pelos semieixos positivos e por uma reta que passa pelo ponto . Dentre todos esses triângulos, aquele que possui área mínima tem a hipotenusa valendo:
Ver solução completaQuestão 107
Um arame de comprimento deve ser cortado em pedaços, um para formar um quadrado e outro um triângulo equilátero. Como se deve cortar o arame para que a soma das áreas cercadas pelos pedaços seja:
máxima?
mínima?
Mostre que no caso o lado do quadrado é da altura do triângulo.
Ver solução completaQuestão 108
Deseja-se construir uma esfera e um cubo de modo que a soma das áreas de suas superfícies seja igual a . Determine o raio da esfera que maximiza e o que minimiza a soma de seus volumes.
Ver solução completaQuestão 109
Um cilindro é obtido girando-se um retângulo ao redor do eixo , onde a base do retângulo está apoiada. Seus vértices superiores estão sobre a curva Qual é o maior volume que tal cilindro pode ter?
Ver solução completaQuestão 110
Sejam e duas retas paralelas com a distância entre eles igual a . Fixe um ponto sobre a reta . Fixe dois pontos e sobre a reta de modo que a distância entre os pontos e seja igual a . É possível encontrar um ponto na reta , de modo que o segmento intercepte o segmento em um ponto de forma que a soma das áreas dos triângulos e seja mínima? E seja máxima? Nos casos em que a resposta for afirmativa, determine a altura do triângulo
Ver solução completaQuestão 111
Sejam . Determine, caso exista, o perímetro mínimo dos triângulos de base e altura (relativa à base dada) .
Ver solução completaQuestão 112
Um muro de metros de altura está a metro de distância da parede lateral de um prédio. Qual o comprimento da menor escada cujas extremidades se apoiam uma na parede, e outra no chão do lado de fora do muro?
Ver solução completaQuestão 113
Sejam um intervalo aberto e uma função derivável. Assuma que vale o seguinte teorema: se , com , então para todo entre e , existe tal que . (Observe que não supomos de classe . Com base nesse teorema podemos afirmar que:
Não existe função , derivável, tal que e para todo .
toda função derivável em possui sua derivada contínua em .
toda função derivável em possui descontínua em todo ponto de .
nenhuma das alternativas anteriores é correta.
Ver solução completaQuestão 114
Determine dois números positivos cuja a soma seja 4 e tal que a soma do cubo do menor com o quadrado do maior seja mínima.
Ver solução completaQuestão 115
Uma caixa em forma de paralelepípedo deve ter comprimento igual ao dobro da largura. Se a soma da altura com a largura deve ser 48 cm, calcule seus valores para que o volume seja máximo.
Ver solução completaQuestão 116
Quais devem ser as dimensões de uma pastagem retangular dede área, feita a margem de um rio reto para que o gasto com a cerca seja o menor possível sabendo que não é necessário fazer cerca ao longo do rio?
Ver solução completaQuestão 119
Um fazendeiro quer cercar uma área de em um campo retangular e então dividi-lo ao meio com uma cerca paralela a um dos lados do retângulo. Como fazer isso de forma que minimize os custos da cerca?
Ver solução completaQuestão 120
Encontre as dimensões do retângulo com a maior área que pode ser inscrito em um círculo de raio r.
Ver solução completaQuestão 121
Uma página retangular deve conter de área impressa. As margens superior e inferior devem ter cada, enquanto as laterais devem ter cada. Encontre as dimensões que deve ter a página para consumir a menor quantidade de papel.
Ver solução completaQuestão 122
Uma certa locadora de automóveis cobra R$ 35,00 por dia mais 55 centavos por quilômetro rodado.
(a) Expresse o custo para alugar um carro nessa locadora por 1 dia em função do número de quilômetros rodados e desenhe o gráfico relacionado.
Ver solução completaQuestão 123
Uma certa locadora de automóveis cobra R$ 35,00 por dia mais 55 centavos por quilômetro rodado.
(c) Quantos quilômetros o carro rodou se o preço do aluguel por 1 dia foi R$ 72,00?
Ver solução completaQuestão 124
Dado o triângulo retângulo de catetos e , determine o retângulo de maior área que está inscrito no triângulo de modo que um dos lados está contido na hipotenusa.
Ver solução completaQuestão 125
Um contêiner para estocagem, retangular sem tampa, deve ter um volume de 10 m³. O comprimento de sua base é o dobro da sua largura. O material para a base
custa R$ 2,50 por metro quadrado. O material para os lados custa R$ 9,00 por metro quadrado. Encontre o valor y da largura do contêiner para que o custo da sua
construção seja o menor possível.
Questão 126
Joga-se uma pedra em um lago, produzindo ondas circulares cujos raios aumentam a uma razão constante de . A que taxa está aumentando a circunferência de uma onda quando o raio é de ?
Ver solução completaQuestão 127
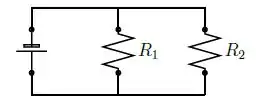
Quando dois resistores e são ligados em paralelo (veja a figura), a resistência total é dada pela equação . Se e estão aumentando as taxas de e respectivamente, a que taxa varia no instante em que e ?
Questão 128
Um triatleta se encontra numa praia reta, a 900 m do Bar do Zé, quando vê uma criança cair de um barco no mar a 300 m da praia, na altura deste bar, como ilustrado abaixo. Se o atleta corre na areia a 500 m/min e nada a 400 m/min, determine o caminho que ele deve escolher para chegar o mais rápido possível ao resgate da criança. Quanto tempo vai demorar para percorrer este caminho? (Obs:300² + 400² = 500²).
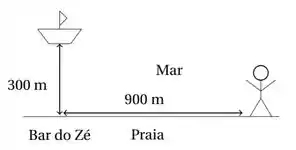
Questão 129
Um tanque tem a forma de um cone circular reto invertido, com metros altura e metros de raio da base. Se a água entra no tanque à razão de , calcule aproximadamente a razão na qual o nível da àgua subindo quando a profundidade é de metro.
Ver solução completaQuestão 130
A área de um triângulo equilátero decresce à razão de . Determine a taxa na qual o comprimento do lado está variando quando a área do triângulo é
Ver solução completaQuestão 131
Suponha que a área total de um tambor cilíndrico sem tampa deve ser . Determine o raio da base e a altura do mesmo para que sua capacidade seja maior possível. Qual é essa capacidade?
Ver solução completaQuestão 132
Um fazendeiro tem de cerca para construir três galpões retangulares adjacentes e com lados medindo e . Quais devem ser as dimensões dos galpões de modo a maximizar a área total cercada?
Ver solução completaQuestão 133
Determine o retângulo de maior área e lado paralelos aos eixos coordenados que está inscrito na elipse .
Ver solução completaQuestão 134
Uma empresa foi fundada em 1990 e sua capacidade de produção P = P (t) evoluiu segundo:
(b) Qual foi essa capacidade?
Ver solução completaQuestão 136
Duas partículas e movem-se, respectivamente, sobre os eixos e . A função de posição de é e a de , , . Determine o instante em que a distância entre e seja a menor possível.
Ver solução completaQuestão 137
Achar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completa