Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 4.7 - Ex. 9

Dadas as funções f x = 1 x - 1 e g x = 2 x 2 - 3 , determinar os itens que seguem e, usando uma ferramenta gráfica, fazer um esboço do gráfico das funções obtidas, identificando o seu domínio.

  1. f ∘ f '
  2. f ' ∘ f
  3. g ∘ f '
  4. g ' ∘ f '

Passo 1

Vamos calcular a derivada de f ' x pela definição:

f ' x = lim ∆ x → 0 ⁡ f x + ∆ x - f x ∆ x = lim ∆ x → 0 ⁡ 1 x + ∆ x - 1 - 1 x - 1   ∆ x =

= lim ∆ x → 0 ⁡ 1 x + ∆ x - 1 - 1 x - 1 ⋅ 1 ∆ x = lim ∆ x → 0 ⁡ x - 1 - x + ∆ x - 1 x + ∆ x - 1 x - 1 ⋅ 1 ∆ x =

= lim ∆ x → 0 ⁡ x - 1 - x - ∆ x + 1 x + ∆ x - 1 x - 1 ⋅ 1 ∆ x = lim ∆ x → 0 ⁡ - ∆ x x + ∆ x - 1 x - 1 ⋅ 1 ∆ x =

= lim ∆ x → 0 ⁡ - 1 x + ∆ x - 1 x - 1 = - 1 x + 0 - 1 x - 1 = - 1 x - 1 2

E agora para g ' x :

g ' x = lim ∆ x → 0 ⁡ g x + ∆ x - g x ∆ x = lim ∆ x → 0 ⁡ 2 x + ∆ x 2 - 3 - 2 x 2 - 3   ∆ x =

= lim ∆ x → 0 ⁡ 2 x 2 + 2 x ∆ x + ∆ x 2 - 3 - 2 x 2 + 3   ∆ x = lim ∆ x → 0 ⁡ 2 x 2 + 4 x ∆ x + 2 ∆ x 2 - 2 x 2 ∆ x =

= lim ∆ x → 0 ⁡ 4 x ∆ x + 2 ∆ x 2 ∆ x = lim ∆ x → 0 ⁡ 4 x + 2 ∆ x = 4 x + 2 ⋅ 0 = 4 x

Passo 2

  1. Vamos calcular f ∘ f ' :

    2. f ∘ f ' = f f ' = f - 1 x - 1 2 = 1 - 1 x - 1 2 - 1 = 1 - 1 - x - 1 2 x - 1 2 = x - 1 2 - 1 - x 2 + 2 x - 1 =

    = x - 1 2 - 2 - x 2 + 2 x

    Temos o gráfico de f ∘ f ' da forma:

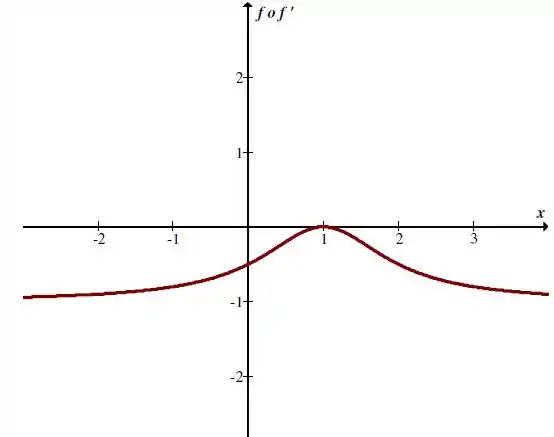
    Passo 3

  2. Vamos calcular f ' ∘ f :

    3. f ' ∘ f = f ' f = f ' 1 x - 1 = - 1 1 x - 1 - 1 2 = - 1 1 - x + 1 x - 1 2 = - 1 - x + 2 x - 1 2 = - x - 1 - x + 2 2

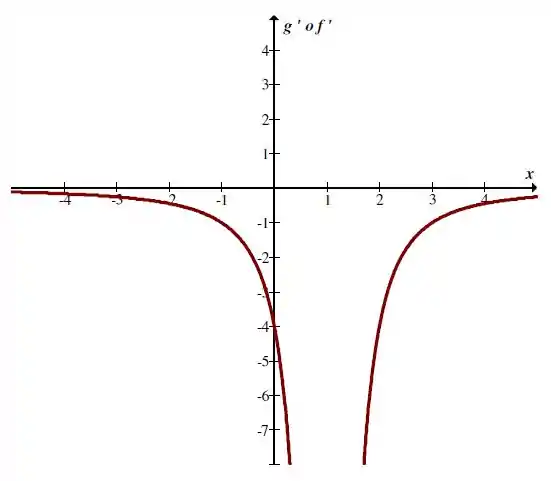
    Temos o gráfico de f ' ∘ f da forma:

    Passo 4

  3. Vamos calcular g ∘ f ' :

    4. g ∘ f ' = g f ' = g - 1 x - 1 2 = 2 - 1 x - 1 2 2 - 3 = 2 ⋅ 1 x - 1 4 - 3 = 2 x - 1 4 - 3

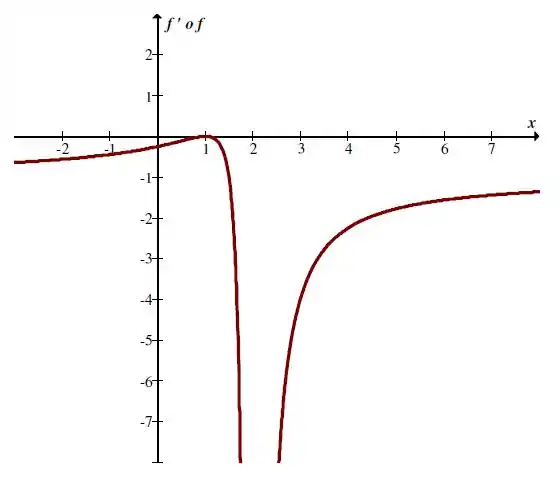
    Temos o gráfico de g ∘ f ' da forma:

    Passo 5

  4. Vamos calcular g ' ∘ f ' :

g ' ∘ f ' = g ' f ' = g ' - 1 x - 1 2 = 4 - 1 x - 1 2 = - 4 x - 1 2

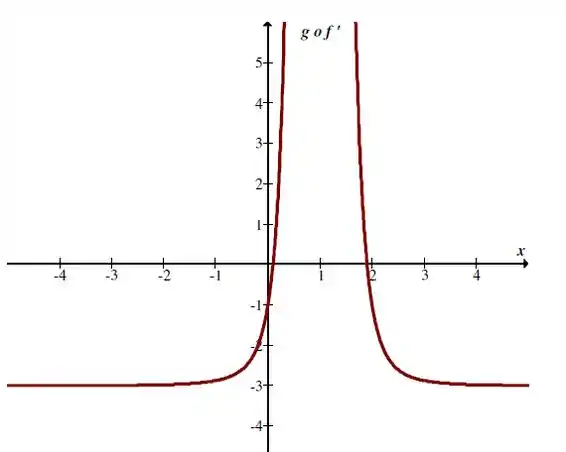
Temos o gráfico de g ' ∘ f ' da forma:

Resposta

  1. f ∘ f ' = x - 1 2 - 2 - x 2 + 2 x
  2. f ' ∘ f = - x - 1 - x + 2 2
  3. g ∘ f ' = 2 x - 1 4 - 3
  4. g ' ∘ f ' = - 4 x - 1 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Calcule o limite:underset(theta - pi // 4)(lim) (t g (theta) - 1)/(theta - (pi)/(4))
Calcule o limite:underset(theta - pi // 6)(lim) (s e n (theta) - (1)/(2))/(theta - (pi)/(6))
Calcule o limite:underset(x - 2)(lim) s e n ((1)/(x) - (1)/(2))
Calcule o limite:underset(x - 0)(lim) sec [e^x + pi * t g ((pi)/(4 sec (x))) - 1]
Nos Exercícios de 25 a 30, ache f ' ( x ) aplicando a fórmula (3).25) f x = 7 x + 3