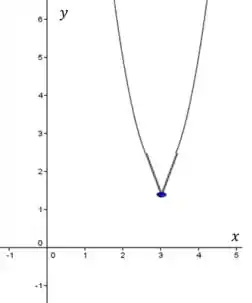
46. Dado que a função é contínua para todos os valores de , , se e se , faça um esboço de um possível gráfico de em cada um dos seguintes casos, onde forem satisfeitas as condições adicionais: (a) é contínua em 3; (b) , se , e , se ; (c) e se .
Passo 1
Vamos olhar as primeiras condições que são comuns a todos os itens e depois avaliamos cada condição adicional.
Passo 2
Bem, temos o seguinte: é contínua para todos os valores de , , se e se . Isso quer dizer, a função é uma linha contínua pra todo valor de , sendo que em , essa função tem valor 2. Outra coisa, pelas derivadas, para, a função é decrescente porque a derivada é negativa, e para é crescente pois a derivada é positiva. Isso vale pros 3 itens
Passo 3
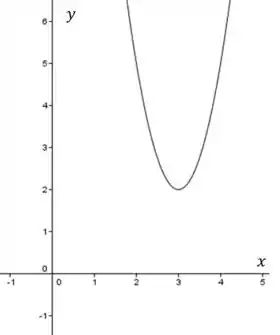
a) é contínua em 3.
Bem, pra isso, a função não pode ter indeterminação nesse ponto nem uma quina, é aí que a curva muda de decrescente para crescente, então um bom esboço é:
Passo 4
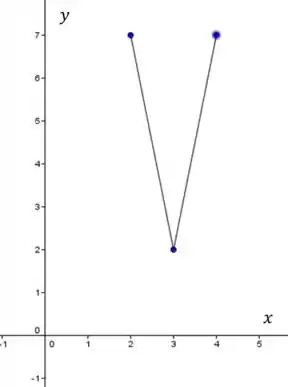
b) , se , e , se
Para que a derivada seja um valor constante, a função precisa ser um reta. Quando a derivada for negativa, a função será uma reta decrescente. Pelo teorema 4.4.3, quando a derivada for positiva, a função será uma reta crescente. Então o esboço fica:
Passo 5
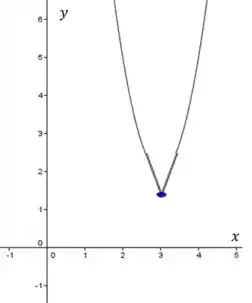
c) e se
Agora, no limite de 3 à esquerda, a derivada é negativa e no limite à direita a derivada é positiva, agora a função continua decrescente para virar crescente (teorema 4.4.3), mas no ponto 3 tem algo como uma quina, por exemplo. E as derivadas dos pontos a e b são diferentes, tranquilo isso, a função assume valores diferentes com nos outros itens. Então o esboço é:
Resposta
a)

b)
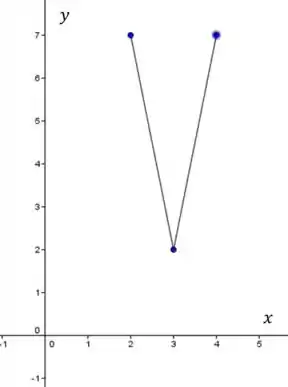
c)