Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 4.4 - Ex. 24
ache os extremos relativos de pelo teste da derivada primeira
determine os valores nos quais os extremos relativos ocorrem
determine os intervalos nos quais é crescente
determine os intervalos nos quais é decrescente
faça um esboço do gráfico
Passo 1
Bem, para realizarmos toda essas analises que ele pediu, precisamos basicamente de uma coisa.
Analisar os sinais da primeira derivada. A partir disso sabemos todo o resto.
A nossa função é:
Primeiro vamos achar a derivada:
Vamos analisar seu sinal agora
Passo 2
Repare que tem um expoente par ali naquele , isso faz com que esse termo seja sempre positivo.
Mas quando multiplicarmos por vai ficar negativo. Então vamos ter:
Que basicamente é ela ser negativa em todos os valores de
Passo 3
Vamos analisar cada uma das coisas que ele pediu.
Para termos extremos relativos precisamos ter mudança de sinal na derivada.
Isso porque a derivada está ligada ao crescimento ou decrescimento da função:
Os extremos existem quando mudamos de crescente para decrescente, que vão ser os pontos de máximo.
E quando mudamos de decrescente para crescente, que vão ser os pontos de mínimo.
Assim, vamos ter:
Não vamos ter extremos porque a derivada não muda de sinal, ela é sempre decrescente.
Passo 4
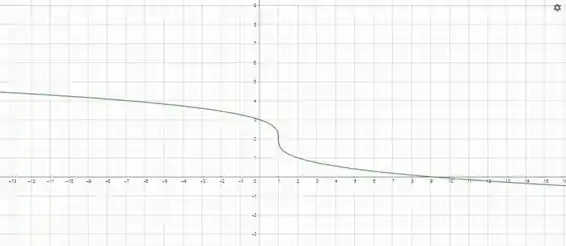
O esboço fica:
Resposta
Não tem extremos
