Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 3 f
O gráfico da função é dado:
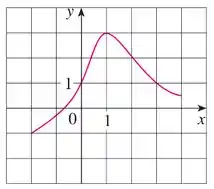
f) Em qual intervalo é crescente?
Passo 1
Então pessoal, estamos quase acabando o exercício, vamos lá!!
O exercício pede para falar em qual intervalo é crescente. O que isso quer dizer?
O intervalo que a função é crescente é quando o valor aumenta toda vez que aumenta um pouquinho.
Assim, uma ideia é montarmos uma tabelinha relacionando e seu valor de correspondente.
Dessa forma podemos perceber os intervalos de crescimento e decrescimento!!
E aí?? Bora lá?? 😉
Passo 2
Na tabela abaixo, temos alguns valores para o e conforme a função:
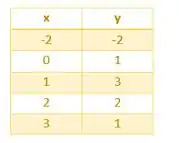
Quando sai de e vai o valor de sai de e vai para , isso quer dizer que aumentou conforme íamos aumentando o
Quando sai de e vai o valor de sai de e vai para , isso quer dizer que diminuiu conforme íamos aumentando o
Passo 3
Então, conforme a definição, podemos concluir que a função é crescente quando
Assim, vendo no gráfico, será essa parte pontilhada que está ascendente:
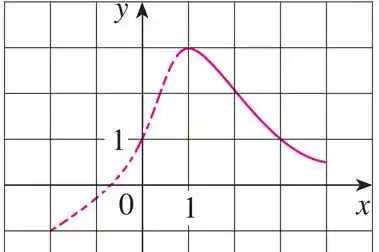
Ufaaa, terminamos pessoal!
Entendeu direitinho?? Responde aee 😉
Resposta
No intervalo