Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 1.1 - Ex. 3 d
O gráfico da função é dado:
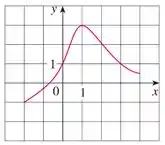
d) Estime os valores de tais que
Passo 1
Eaee, belezinha?? Bom, a questão nos dá o seguinte gráfico de uma função :
A questão quer que encontremos o valor de onde .
Para isso, vamos marcar o ponto e traçar uma reta uma reta paralela ao eixo ate encostar na curva, quantas vezes for necessário.
Então bora lá!! 😉
Passo 2
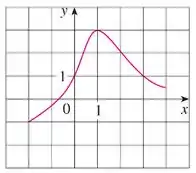
Agora, teríamos que fazer o mesmo que fizemos na questão anterior, certo?
Marcando os pontos de interseção, temos:
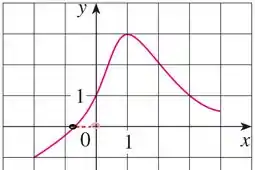
Passo 3
Temos só um , não é ? Certo. Então agora é só trace uma reta vertical paralela ao eixo dos pontos de interseção ate ao eixo
Perceba que essa reta, não vai existir, porque a curva já toca no eixo diretamente, então esse ponto em que a curva toca no eixo é o ponto que precisamos, certo?
Que é o ponto
Aqui vai uma dica: Sempre que pedir o valor de em que temos que é o valor que o gráfico corta o eixo .
Entendeu direitinho?? Responde aee 😉