Enunciado
Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.3 - Ex. 62
A Desigualdade Triangular para vetores é:
- De uma interpretação geométrica para a Desigualdade Triangular.
- Use a Desigualdade De Cauchy-Schwarz do Exercício 57 para demonstrar a Desigualdade Triangular. [Sugestão: Use o fato de que e utilizr a Propriedade 3 do produto escalar].
Passo 1
Bom, se isso é uma desigualdade TRIANGULAR, tem a ver com triangulo. Então vamos pensar em e como lados de um triângulo.
Se a gente fizer a soma do vetor com o vetor , temos, geometricamente, um triangulo assim:
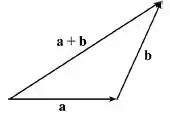
A desigualdade diz que o tamanho do vetor , que é o lado maior do triangulo, é menor ou igual a soma dos outros dois lados menores do triângulo.
Belezinha?
Passo 2
Vamos começar usando a sugestão dele:
Além disso, a Desigualdade De Cauchy-Schwarz diz que
Substituindo essa desigualdade ali em cima, ficamos com:
E isso é a cara de um quadrado perfeito!!!
Já estamos quase chegando na desigualdade triangular! Falta só tirar a rai dos dois lados, asism:
UHUL!
Resposta
A desigualdade diz que o tamanho do vetor , que é o lado maior do triangulo, é menor ou igual a soma dos outros dois lados menores do triângulo.