Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 12.2 - Ex. 7

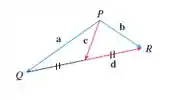
Na figura, a ponta de c e a cauda de d são ambas o ponto médio de QR. Expresse c e d em termos de a e b.

Passo 1

Pela figura, podemos deduzir inicialmente que para o segmento Q R - , temos Q R - = 2 d , então pela lei do triângulo:

a + 2 d = b

2 d = b - a

Logo,

d = 1 2 ( b - a )

Novamente, pela lei do triângulo:

c + d = b

Então,

c + 1 2 b - 1 2 a = b

c = b - ( 1 2 b - 1 2 a )

c = 1 2 a + 1 2 b

Prontinho!!

Resposta

c = 1 2 a + 1 2 b   e d = 1 2 ( b - a ) .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

u →=( 2,1 , - 3 ) e v →=( 1,2 , 1 ) . Se w →=u→+λ v → , determine λ para que u→ e w → sejam ortogonais.Determine o coseno do ângulo que u→ forma com v → .
Sejam O A →=( 1,1 , 3 ) , O B →=( 3,2 , 2 ) e O C →=( 1,0 , - 4 ) .Ache as coordenadas de todos os vetores determinados pelos pontos O, A, B e C.Demonstre que os 4 pontos (não necessariamente na ordem
Ache um vetor v → que forma ângulos iguais com ( 1,0 , 0 ) e ( 0,0 , 1 ) é ortogonal a u →=( 2 , - 2,2 ) , | v | →= 24 , sendo agudo o ângulo que v → forma com ( 0,1 , 0 ) .
Ache um vetor de norma 1, ortogonal a u →=( 1 , - 3,1 ) e a v →=( - 3,3 , 3 ) .
Determine o vetor u → sabendo que u → é combinação linear de ( 1 , - 3,0 ) e ( 0 , - 4,1 ) , u → é ortogonal a ( 0,1 , - 2 ) , | u | →=3 e u → forma um ângulo obtuso com k →= ( 0,0 , 1 ) .