Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.4 - Ex. 24

Determine se a afirmação dada é verdadeira ou falsa. Explique sua resposta.

Dada qualquer função contínua f , a área entre o gráfico de f em um intervalo [ a , b ] (no qual f estiver definida) é igual ao valor absoluto da área líquida com sinal entre o gráfico de f e o intervalo [ a , b ] .

Passo 1

Falso. Só seria verdadeiro para casos em que f ≥ 0 em todo o intervalo. Nos casos onde f assume valores abaixo do eixo também, a área líquida será a diferença entre a área da parte positiva e a negativa, e não corresponde á área sobre o gráfico propriamente dita.

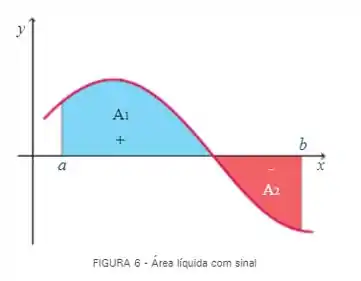
A área líquida com sinal pode ser positiva, caso a parte azul seja maior que a vermelha; negativa se a parte vermelha for maior; ou até nula se as duas forem iguais. Portanto, nesses casos, não representa a área entre o gráfico.

Resposta

Falsa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos exercícios de 1 a 14, ache o limite e, quando aplicável, indique os teoremas de limite usados. 13 )lim x → 4 ⁡ x ² - 3 x + 4 2 x ² - x - 1 3 ² ²
Nos exercícios de 15 a 20, faça o seguinte:Use uma calculadora para tabular, até quatro casas decimais, os valores de f ( x ) para os valores fixados de x . Do que f ( x ) parece tender quando x se ap
Nos exercícios de 15 a 20, faça o seguinte:Use uma calculadora para tabular, até quatro casas decimais, os valores de f ( x ) para os valores fixados de x . Do que f ( x ) parece tender quando x se ap
Nos exercícios de2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 21 )lim x → 7 ⁡ x 2 - 49 x - 7
Nos exercícios de2 1 a 39, encontre o limite e, quando aplicável, indique os teoremas de limite usados. 26 )lim x → 4 ⁡ 3 x 2 - 17 x + 20 4 x ² - 25 x + 36 ²