Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 1.5 - Ex. 18

Determine o domínio e a imagem da função e desenhe um esboço do seu gráfico.

g x = x 3 - 3 x 2 - 4 x + 12 x 2 - x - 6

Passo 1

A questão quer que determinemos os valores que x pode assumir e os valores que podem retornar em y da função. A questão também quer o gráfico da função, mas desse jeito que a função está, fica complicado determinar qualquer coisa. Vamos tentar simplificar algumas coisas. Vamos tentar fatorar o polinômio do numerador e o do denominador. Começando pelo denominador que é mais fácil:

x 2 - x - 6 = x - x 1 x - x 2

Podemos reescrever o polinômio do denominador dessa forma, onde x 1 e x 2 são as raízes da equação quadrática.

Por bhaskara podemos encontrar essas duas raízes:

x 1,2 = - - 1 ± - 1 2 - 4 ∙ 1 ∙ - 6 2 1

x 1,2 = 1 ± 25 2

Daí temos nossas 2 raízes:

x 1 = 3

E

x 2 = - 2

Então temos o denominador fatorado com sucesso:

x 2 - x - 6 = x + 2 x - 3

Já podemos reescrever a função como:

g x = x 3 - 3 x 2 - 4 x + 12 x + 2 x - 3

Passo 2

Agora vamos encarar esse numerador, um passo de cada vez

x 3 - 3 x 2 - 4 x + 12

Vamos colocar - 4 em evidência nos dois últimos termos:

x 3 - 3 x 2 - 4 ( x - 3 )

Botando o x 2 em evidência nos dois primeiros temos:

x 2 x - 3 - 4 x - 3

Temos ( x - 3 ) nos dois termos! Vamos colocar ele em evidenciaem evidência!

x - 3 x 2 - 4

x 2 - 4 é o mesmo que x 2 - 2 2 que é uma diferença de quadrados! Podemos escrever uma diferença de quadrados como:

a 2 - b 2 = a + b a - b

Só que pra nós, a = x e b = 2 . Vamos reescrever:

( x - 3 ) ( x + 2 ) ( x - 2 )

Numerador fatorado com sucesso!

x 3 - 3 x 2 - 4 x + 12 = x - 3 x + 2 x - 2

Substituindo isso na função:

g x = x - 3 x + 2 x - 2 x + 2 x - 3

Agora podemos dar aquela simplificada de mestre!

g x = x - 2

Passo 3

A nossa função nada mais é do que uma reta! Então ela está definida para todo x e também pode resultar em qualquer valor de y ! Então nosso domínio é ( - ∞ ,   + ∞ ) e a imagem também!

Passo 4

Agora só falta o gráfico da função. Para plotar o gráfico de uma reta é muito simples: precisamos de dois pontos quaisquer. Vamos fazer g ( 0 ) e g ( 1 ) para encontrar esses dois pontos:

g 0 = 0 - 2 = - 2

g 1 = 1 - 2 = - 1

Temos os dois pontos: ( 0 ,   - 2 ) e ( 1 ,   - 1 ) . No plano cartesiano eles ficam:

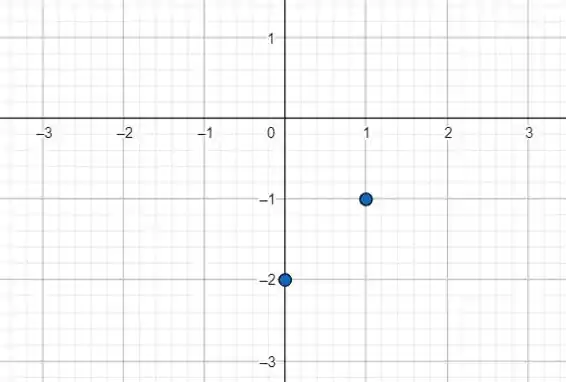
Agora só precisamos da reta que liga esses dois pontos! Fica assim ó:

`

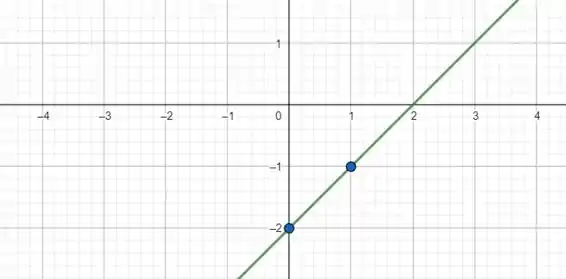Essa reta verde é o gráfico da g ( x ) !

Resposta

Domínio: ( - ∞ ,   + ∞ )

Imagem: ( - ∞ ,   + ∞ )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = 5 x 2 / 5 - 2 x
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = x 2 - 1
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = 1 - 1 x + 3
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = x 2 - x
Determine uma janela de visualização apropriada para a função dada e a utilize para exibir o gráfico da função: y = x + 3 x + 2