Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.1 - Ex. 76
Determine se é par, ímpar ou nenhum dos dois. Se você tiver uma calculadora gráfica, use-a para verificar visualmente sua resposta.
Passo 1
Fala aí! Tudo certinho? 👀
Nesse problema temos que verificar se é uma função impar ou uma função par.
Lembra como fazemos isso? 😬
A gente analisa se é ímpar ou par substituindo por e analisando se obtemos , ou nenhuma das duas.
Uma função par possui simetria em relação ao eixo e uma função par possui simetria em relação à origem do sistema.
Veja só! 😉
Passo 2
Assim, temos que
Portanto, , sendo assim uma função ímpar.
Visualmente temos a seguinte figura:
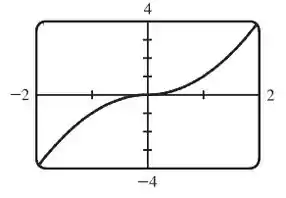
O gráfico nos confirma que é realmente uma função ímpar, pois gira em torno do eixo partindo origem e gira em torno do eixo , como um espelho de cabeça para baixo.
Legal, né? O que achou? Responde Aí! 😁
Resposta
é uma função ímpar.