Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 1.1 - Ex. 39
1.45. Encontre o domínio e esboce o gráfico da função.
Passo 1
Falaaa... tudo bem??
Nessa questão vamos encontrar o domínio e esboçar o gráfico da função:
Pra encontrar o domínio de uma função a gente vê se tem algum dos casos de restrição:
- divisão por zero: se a função tiver algo envolvendo no denominador, vamos calcular pra qual valor a expressão do denominador vale zero e tiramos esse valor do domínio.
- raiz de número negativo: quando temos uma raiz quadrada, a expressão que tem dentro da raiz ela só pode ser maior ou igual a zero,, então calculamos quais os valores de que satisfazem essa condição e achamos o domínio.
- logaritmo de número não positivo: quando temos log, a expressão que está dentro do log deve ser sempre maior que zero. Dessa restrição achamos o domínio.
Passo 2
Pra começar, vamos olhar bem nossa função. Veja que ela tem um módulo! Então vamos precisar pescar a definição de módulo:
Agora, que tal somar pras duas definições?
E dividindo as duas defini��ões por :
Nota uma coisa importantíssima agora! Se eu dividi por , então eu tenho que transformar em ! Afinal, não posso dividir nada por zero! Vemos então que nessa função, o zero não está definido! Cortando os nas definições, chegamos a:
Passo 3
E esse é o nosso último passo galera! Como:
O gráfico fica o seguinte:
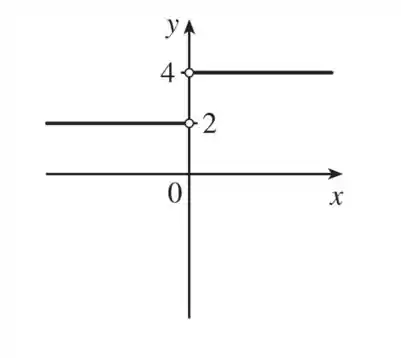
E essa bolinha branca é bem importante viu? Ela mostra que nem é igual a e nem igual a ! Afinal, é indefinido! Pra qualquer outro valor de , a função ou assume o valor ou o . Portanto o domínio é:
Resposta
