Encontre o domínio e esboce o gráfico da função:

Vamos começar com o domínio:

A única restrição que temos é que o denominador não pode ser zero (divisão por zero não existe!)! Logo, teremos que:

Podemos então concluir que:

Fechou? Então o nosso domínio é o conjunto de todos os números reais , menos o zero. Em linguagem matemática, a gente escreve isso assim:

Para fazer o gráfico da função temos que, primeiro, “abrir” o módulo em duas outras funções (uma que vai ser positiva e outra negativa). Dá uma olhada:

Beleza? Como temos em cima e em baixo em cada uma das expressões que a gente achou, podemos dar uma simplificada. Vai ficar assim:

Bom, agora que já demos uma mexida na nossa função , dá pra ver que ela é composta por duas funções do tipo , certo? O gráfico dessa função é característico e muito bem conhecido, daquelas que a gente tem que saber de cabeça! Esse gráfico é chamado de hipérbole.

Como o esta no denominador, a medida que o módulo de cresce o fica muito pequeninho, próximo de zero. E quando o módulo de se aproxima de zero cresce muito! Vamos testar:

Com essa reflexão, se você não lembrava como que é a carinha do gráfico tipo hipérbole, já deu pra relembrar né!

Além disso, o nunca vai tocar o eixo , pois pra isso teríamos que ter e pelo mesmo motivo nunca vai tocar o eixo .

Agora só vamos pegar mais dois pontinhos chaves:

O gráfico de vai ser, então, composto por duas partes: uma devido a e outra devido a (o sinal de menos vai refletir o gráfico com relação ao eixo vertical). O nosso gráfico final vai ficar assim:

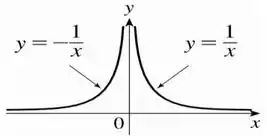
E aí a gente termina a nossa questão!