Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.8 - Ex. 48

  1. Se g x = 1 x - 1 , use sua calculadora ou computador para fazer uma tabela de valores aproximados de ∫ 2 t g x d x para t = 5 , 10 , 100 , 1   000 e 10   000 . Parece que ∫ 2 ∞ g x d x é convergente ou divergente?
  2. Use o Teorema da Comparação com f x = 1 x para mostrar que ∫ 2 ∞ g x d x é divergente.
  3. Ilustre a parte (b) colocando em um gráfico f e g na mesma tela para 2 ≤ x ≤ 20 . Use seu gráfico para explicar intuitivamente por que ∫ 2 ∞ g x d x é divergente.

Passo 1

  1. Usando uma calculadora vamos achar os valores na tabela abaixo:

    2. t

    ∫ 2 t g x d x

    5

    3,830327

    10

    6,801200

    100

    23,328769

    1000

    69,023361

    10000

    208,124560

    Parece que ∫ 1 ∞ g x d x é divergente, cada vez que aumentamos o valor de t o valor da integral vai sempre aumentando.

    Passo 2

  2. Vamos lá, o Teorema da Comparação diz que:

    3. Supondo que f e g são contínuas com f x ≥ g x ≥ 0 para x ≥ a , se ∫ a ∞ g x d x é divergente, então ∫ a ∞ f x d x é divergente.

    Temos que para x ≥ 2 :

    x > x - 1 → 1 x < 1 x - 1

    Pronto, temos que:

    ∫ 2 ∞ g x d x = ∫ 2 ∞ 1 x d x = ∫ 2 ∞ 1 x 1 2 d x

    Temos que essa integral é divergente, pela equação 2 , que fala que:

    ∫ 1 ∞ 1 x p d x é convergente se p > 1 e divergente se p ≤ 1 .

    Pronto, temos que 0 ≤ g x ≤ f x , assim ∫ 2 ∞ 1 x - 1 d x é divergente.

    Passo 3

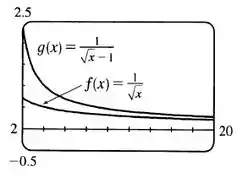
  3. Vamos lá, dá pra ver no gráfico que ∫ 2 ∞ f x d x é infinito, e a área abaixo de g x é maior que a área abaixo de f x no intervalo 2 , t , assim ∫ 2 ∞ g x d x deve ser infinita, o que torna a integral divergente.

Resposta

  1. Parece que ∫ 2 ∞ g x d x é divergente
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Esboce a região e encontre sua área (se a área for finita). S = x , y- 2x ≤ 0 ,0 ≤ y ≤ 1 x + 2 }
Esboce a região e encontre sua área (se a área for finita). S = x , y x ≤ 1 ,0 ≤ y ≤ e x }
Esboce a região e encontre sua área (se a área for finita). S = x , y x ≥ - 2 ,0 ≤ y ≤ e - x / 2 }
Esboce a região e encontre sua área (se a área for finita). S = x , y|0 ≤ y ≤ 2 x 2 + 9
Mostre que ∫ 0 ∞ e - x 2 d x = ∫ 0 1 - ln ⁡ y d y interpretando as integrais como áreas.