Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 12.6 - Ex. 14

Determine o traço da superfície dada nos planos x = k ,   y = k , z = k . Identifique a superfície e faça um esboço dela.

z = x 2 - y 2

Passo 1

O Traço para x = k   s e r á   z = k 2 - y 2

z - k 2 = y 2   que são parábolas.

O Traço para y = k   s e r á   z = x 2 - k 2       que são parábolas.

O Traço para z = k   s e r á   k = x 2 - y 2   que são hipérboles.

Passo 2

Portanto essa superfície é um parabolóide hiberbólico com ponto de sela ( 0,0 , 0 )

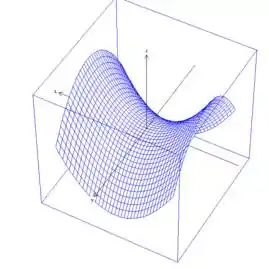
Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1 . Determine o plano tangente à superfície dada, no ponto dado. σ( u ,v )=( u ,v ,u 2+v 2 ) ,n op o n t oσ( 1 ,1 ) . σ( u ,v )=( cos ⁡ u , sin ⁡ u , v ) ,n op o n t oσ( π 2 ,1 ) . σ( u ,v )=( 2 u+v ,
Descreva e esboce a superfície. y 2 + 4 z 2 = 4
Nos exercícios 1 a 6 , esboce o gráfico da superfície de equação dada. x + 2 y - 6 = 0 .
Nos exercícios 1 a 6 , esboce o gráfico da superfície de equação dada. 2 z - 5 y - 1 0 = 0 .
Nos exercícios 1 a 6 , esboce o gráfico da superfície de equação dada. 3 x - 2 z - 12 = 0 .