Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.1 - Ex. 17

Differential equations have been used extensively in the study of drug dissolution for patients given oral medications. One such equation is the Weibull equation for the concentration C T   of the drug:

d c d t = k t b ( c s - c )

where k and c s are positive constants and 0 < b < 1 . Verify that

c t =   c s ( 1 -   e - α t 1 - b )

is a solution of the Weibull equation for t > 0, where   α = k 1 - b . What does the differential equation say about how drug dissolution occurs?

Passo 1

Bem precisamos antes de tudo manipular essa equação. Ela está escrita de um jeito não pratico

d c d t = k t b ( c s - c )

E sabendo que

c t =   c s ( 1 -   e - α t 1 - b )

Então podemos escrever que

d c d t = k t b c s - c s 1 -   e - α t 1 - b

d c d t = k t b c s 1 - 1 +   e - α t 1 - b

d c d t = k t b c s   e - α t 1 - b

Agora sim, podemos fazer a derivada de C

c t =   c s ( 1 -   e - α t 1 - b )

d c d t = C s -   e - α t 1 - b *   - α 1 - b * t - b

Podemos usar que

α = k 1 - b

Então nossa conta fica

d c d t = C s e - α t 1 - b * k 1 - b 1 - b * t - b

d c d t = c s k t b   e - α t 1 - b

Que é exatamente nossa Equação do enunciado. Então acabamos de provar que é realmente solução.

Passo 2

Agora para ajudar a gente a analisar essa equação podemos fazer o seguinte. Plotar o gráfico de C

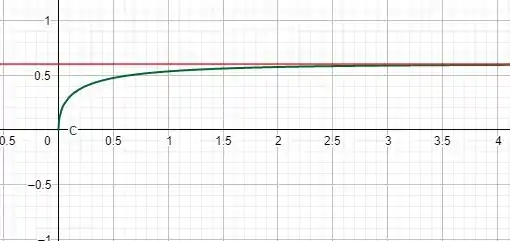
A curva C em verde é nossa concentração. A vermelha é nossa assíntota que é nosso valor de C s . Podemos dizer que A concentração da droga chega a seu valor máximo muito rápido devido a função exponencial. E que conforme k for aumentando, mais rápido essa concentração satura. Nesse gráfico acima usei k = 1 . Se mudarmos para k = 3   temos

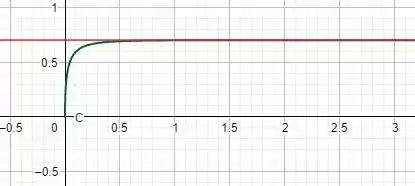
Prontinho Terminamos por aqui. Te vejo na próxima resolução : )

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de y quando t → ∞ . Se esse comportamento dep