Enunciado
Cálculo - Boyce - Equações Diferenciais - Ed: 10º - Capítulo 1.1 - Ex. 33
Em cada um dos problemas de 26 a 33, desenhe um campo de direções para a equação diferencial dada. Baseado no campo de direções, determine o comportamento de quando . Se esse comportamento depender do valor inicial de descreva essa dependência. Note que a expressão à direita do sinal de igualdade nessas equações depende de , além de ; portanto,suas soluções podem exibir um comportamento mais complicado do que as no texto
Passo 1
Campos de direções são ferramentas valiosas no estudo de soluções de equações diferenciais da forma
Em que é uma função dada de duas variáveis, , algumas vezes chamada de função taxa. Um campo de direções pode ser constuido calculando em cada ponto de uma malha retangular. Em cada ponto da malha desenha-se um pequeno segmento de reta cujo coeficiente angular é o valor da função naquele ponto.
Um campo de direções fornece uma boa ideia do comportamento global das soluções de uma equação diferencial.
Passo 2
Agora, vamos caluclar para alguns pontos aleatórios e depois plotar o nosso campo
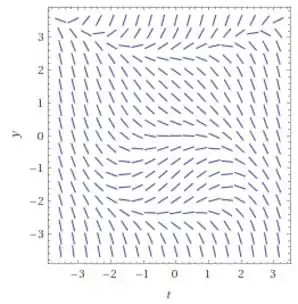
De modo que nosso gráfico tem a seguinte cara
Passo 3
Portanto, ao observarmos o gráfico, vemos que ou ele tende a quando t tende ao infinito.