Os economistas usam uma distribuição acumulada chamada curva de Lorenz para descrever a distribuição de renda entre as famílias em um dado país. Tipicamente, uma curva de Lorenz é definida no intervalo , tem extremidades e e é contínua, crescente e côncava para cima. Os pontos sobre essa curva são determinados classificando-se todas as famílias pela renda e então calculando a porcentagem de famílias cuja renda é menor ou igual a uma porcentagem dada da renda total do país. Por exemplo, o ponto está sobre a curva de Lorenz se de famílias recebe menos do que ou igual a da renda total. A igualdade absoluta da distribuição de renda ocorreria se a parte mais baixa das famílias recebesse da renda e, nesse caso, a curva de Lorenz seria a reta . A área entre a curva de Lorenz e a reta mede quanto a distribuição de renda difere da igualdade absoluta. O coeficiente de desigualdade é a razão da área entre a curva de Lorenz e a reta para a área sob .

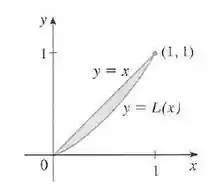
1. Mostre que o coeficiente de desigualdade é o dobro da área entre a curva de Lorenz e a reta , isto é, mostre que o coeficiente de desigualdade
2. A distribuição de renda para um certo país está representada pela curva de Lorenz definida pela equação

Qual a porcentagem da renda total recebida pelas das famílias que recebem menos? Encontre o coeficiente de desigualdade.

Temos que o coeficiente de desigualdade é a razão da área entre a curva de Lorenz e a reta para a área sob , vamos achar a área entre a curva de Lorenz e a reta subtraindo a área abaixo de e abaixo de :

Temos então que o coeficiente de desigualdade é:

Simplificando...

Portanto:

Show?

Para achar a porcentagem da renda total recebida pelas das famílias que recebem menos é só fazer :

Assim, as das famílias que recebem menos recebem da renda total.

Tranquilo até aqui?

Para achar o coeficiente de desigualdade devemos resolver a integral:

Podemos abrir a soma em duas integrais:

Vamos agora calcular a integral indefinida e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração:

Agora é fácil achar as primitivas de cada função, usando duas expressões da Tabela de Integrais Indefinidas:

Bora lá!

Agora é só aplicar, vamos resolver elas separadamente, assim fica mais simples de ver:

Para o outro termo, temos

Pronto, já encontramos a integral indefinida, perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral, agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:

Ficamos então com:

Simplificando...

E fim! O que achou? Responde Aí!