Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Um curso de Cálculo Volume 1 - 5ª Edição - Hamilton Luiz Guidorizzi- Ed: 5º - Capítulo 1.3 - Ex. 5a

Elimine o módulo.

|x + 1| + |x|

Passo 1

Temos pela definição que:

|x| = {[[x s e x >= 0],[- x s e x < 0]])

Basicamente isso fala que para todo x , |x| >= 0 , ou seja, o módulo de um número real é sempre positivo, assim podemos calcular.

Vamos analisar os sinais das expressões dentro dos módulos:

Para x + 1 temos:

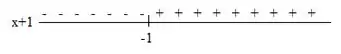
Aqui a expressão assume valores negativos quando x < - 1 e assume valores positivos quando x > - 1 .

Para x temos o seguinte esquema:

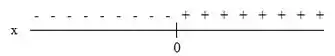
A expressão assume valores negativos quando x < 0 e assume valores positivos quando x > 0 .

Passo 2

Vamos analisar as duas imagens que achamos no passo anterior:

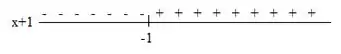
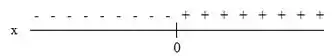
Vamos analisar os três casos, com x <= - 1 , - 1 < x < 0 e x >= 0 .

Com x <= - 1 temos que x + 1 <= 0 e x < 0 , assim a expressão é equivalente a:

|x + 1| + |x| = - (x + 1) - x = - x - 1 - x = - 2 x - 1

Passo 3

Com - 1 < x < 0 temos que x + 1 > 0 e x < 0 , assim a expressão é equivalente a:

|x + 1| + |x| = x + 1 - x = 1

Passo 4

Por último, com x >= 0 temos que x + 1 > 0 e x >= 0 , assim a expressão é equivalente a:

|x + 1| + |x| = x + 1 + x = 2 x + 1

Juntando então temos que:

|x + 1| + |x| = {[[- 2 x - 1 s e x <= - 1],[1 s e - 1 < x < 0],[2 x + 1 s e x >= 0]])

Resposta

x |x + 1| + |x| = {[[- 2 x - 1 s e x <= - 1],[1 s e - 1 < x < 0],[2 x + 1 s e x >= 0]])

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Elimine o módulo. - a , a0
Elimine o módulo. - 5 + - 2
Elimine o módulo. a , a0
Elimine o módulo. 2 a - 3 a
Resolva as equações. 2 x + 3 = 0