Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 8.11 - Ex. 62

Encontrar a área da região interior ao círculo r = 10 e à direita da reta r c o s   θ = 6

Passo 1

A área pedida está na figura:

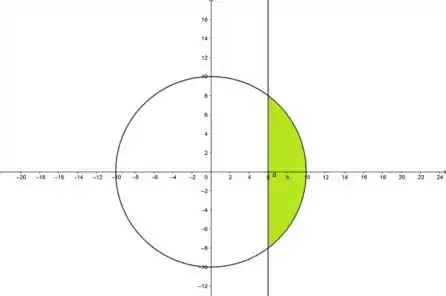
Isolando o r nas duas, a gente tem r = 10 e r = 6 c o s θ .

A interseção acontece em:

10 = 6 cos ⁡ θ

cos ⁡ θ = 6 10 = 3 5

Ou seja, o intervalo vai de [ - arccos ⁡ 3 5 , arccos ⁡ 3 5 ] ,   mas como é simétrico em relação ao eixo x , podemos fazer de 0 , arccos ⁡ 3 5 e multiplicar por 2.

Passo 2

A gente usa a fórmula:

A = 1 2 ∫ α β f θ 2 d θ  

Aí no nosso caso, temos:

A = 2 ∙ 1 2 ∫ 0 arccos ⁡ 3 5 10 2 - 6 cos ⁡ θ 2 d θ

= ∫ 0 arccos ⁡ 3 5 100 - 36 sec 2 ⁡ θ d θ  

[ 100 θ - 36   t g   θ ] 0 arccos ⁡ 3 5

100 arccos ⁡ 3 5 - 48   u . a

Prontinho! Essa é a área que pediram😉

Resposta

100 arccos ⁡ 3 5 - 48   u . a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 20. r = 4 s e n 5 θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 16. r = 3 - 4 c o s θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 11. r = 2 + 2 s e n θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 17. r = 4 + 2 s e n θ
Nos Exercícios de 1 a 36, faça um esboço do gráfico da equação dada 19. r = 2 s e n 3 θ