Seja a função definida pelo gráfico:

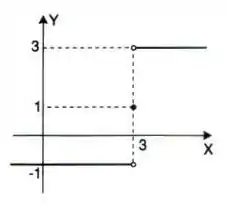
Intuitivamente, encontre se existir:

c)

Então pessoal, o que o enunciado quer é que observemos o gráfico e tentemos concluir se há algum valor para o qual a função tende quando se aproxima de . Se observamos o gráfico, notamos que para o valor da função é . Tudo bem, até aí não há problema! No entanto, aqui temos que fazer uma análise de quanto está tendendo a pela esquerda e pela direita!

Quando pela esquerda, temos que , certo? Ademais, quando pela direita, temos que . Note que os valores foram diferentes para os caminhos possíveis de , sendo assim podemos concluir que o limite da função em não existe! Para existir os limites laterais deveriam ter dado a mesma coisa, logo:

Então é esse nosso resultado! 😉