Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 7.3 - Ex. 43
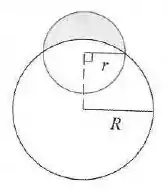
Encontre a área da região em forma de lua crescente delimitada pelos arcos de raios e .
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar a área da região em forma de lua crescente, que é limitada pelo arco de raio e pelo arco de raio .
Vamos fazer outro esboço da situação, pra gente conseguir ver melhor o que ta acontecendo
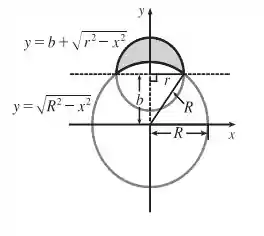
Repare que nós temos um cículo maior e um círculo menor criando a nossa área. Assim, usando as equações dos círculos, vamos definir o nosso integrando e calcular a área através da integral.
Vamos lá!
Passo 2
Vamos começar escrevendo a equação do círculo maior:
Agora, do círculo menor (note que ele não esta centrado na origem:
Na figura, podemos ver que é a hipotenusa do triangulo retângulo que tem e como catetos, então podemos escrever da seguinte forma:
Vamos deixar as equações dos círculos como em função de . Assim, temos:
E
Passo 3
Vamos agora, calcular finalmente a área:
Note que ir de até é o mesmo que ir de até duas vezes. Então, usando a simetria, reescrevemos nosso intervalo de integração:
Agora, como a integral da soma é igual a soma das integrais, temos:
Assim, vamos calcular separadamente cada integral.
Passo 4
Na primeira, teremos:
Como é uma constante:
Aplicando os limites de integração:
Passo 5
Na segunda integral:
Vamos fazer a substituindo trigonométrica:
Dessa forma, temos:
Calculando os novos limites de integração e substituindo na integral, ficamos com:
Agora substituindo tudo na integral:
Colocando em evidência:
Usando a identidade e simplificando, temos:
Fazendo o produto dos termos:
Agora usando a identidade :
E integrando, teremos:
Aplicando os limites de integração:
Passo 6
Agora, calculando a ultima integral (analogamente a segunda), temos que:
Vamos fazer , de modo que . Assim, calculando os novos limites de integração:
E substituindo na integral, ficamos com:
Usando a identidade e simplificando, temos:
Agora usando a identidade :
E integrando, teremos:
Passo 7
Antes de aplicar os limites de integração, vamos encontrar agora uma expressão para e :
Da resolução, vimos que :
Então, substituindo no resultado da integral do passo anterior, temos:
Simplificando:
E aplicando os limites do intervalo:
Passo 8
Agora, basta juntarmos o resultado das 3 integrais:
E encontramos nosso resultado.
Valeu, galera! Até a próxima! 😉