Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 5.9 - Ex. 19
Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da região como o limite de uma soma de Riemann; (c) ache o limite na parte (b), calculando uma integral definida pelo segundo teorema fundamental do Cálculo.
19. ; ;
Passo 1
Vamos olhar as curvas e colocar num gráfico a região delimitada por elas com o elemento retangular. Depois escrevemos o limite por soma de Riemann e por fim, calculamos esse limite.
Passo 2
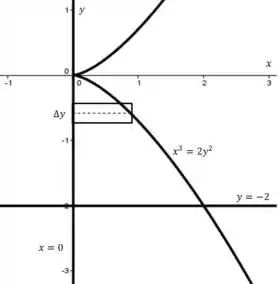
a) Colocando no gráfico, teremos:
Onde o representa uma partição do intervalo [] no eixo . ;)
Passo 3
b) Para um soma de Riemann, pela definição 5.5.1, temos:
(no caso é o valor da nossa área )
Mas como assim? Precisamos calcular os retângulos sob a curva e somá-los para então obter a área sob a curva. Então, a área de cada retângulo é , onde é a nossa função que tá por cima mas num ponto que pertence a . A norma da partição é ||||, quando o limite disso tende a zero, muitos retângulos “finos” serão calculados, melhorando o cálculo da área. Certinho? Vamos escrever esse limite...
A altura dos mini retângulos será a função .
Show? =]
Passo 4
c) Agora vamos calcular esse limite
Pela definição 5.5.2 esse limite pode ser calculado como uma integral de , assim ó:
Resolvendo...
Prontinho, calculamos a área pela soma de Riemann e deu a mesma coisa :D
Resposta
a)
b)
c)