Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.1 - Ex. 41
Encontre o domínio e esboce o gráfico da função
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado quer que a gente esboce o gráfico e encontre o domínio da seguinte função:
Mas o que é esse domínio??
Bom... Determinar o domínio da função é o mesmo que dizer quais valores de podemos por na função sem que haja nenhum problema. Ou seja, são os valores de para os quais a nossa função está definida.
A gente tem sempre que procurar por valores que nos gerem uma indeterminação, que façam a nossa função não existir. Esses valores podem ser números que deixem um denominador igual a zero ou que façam uma raiz de índice par ter o radicando negativo. Além disso, lembre-se que funções polinomiais, em geral, são definidas para todos os valores de .
Com tudo isso em mente, vamos analisar a nossa função e esboçar seu gráfico no plano cartesiano.
Vamos lá!
Passo 2
Vamos primeiro analisar o domínio, certo?
Precisamos determinar quais valores de podemos por na função sem que haja nenhum problema. Analisando bem, essa função não tem problema nenhum, pois não há risco de dividir por zero e nem calcular raiz quadrada negativa, por exemplo.
Observe que ela é uma função polinomial, definida para todos os valores reais. Então o nosso domínio é o conjunto dos números reais, ou seja:
Passo 3
Agora, temos que esboçar o gráfico. Então, vamos analisar o comportamento da nossa função.
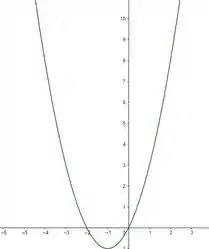
Observe que é uma função quadrática, que é representada geometricamente por uma parábola. Nesse caso, temos uma concavidade para cima, pois o termo que acompanha o é positivo.
Se fizermos temos , indicando que ela toca o eixo nesse ponto. Já para temos e , indicando as raízes da nossa equação, que são os pontos onde ela toca o eixo .
Assim, esboçando a função, vamos ter:
Valeu, galera! Até a próxima! 😉