Esboce o gráfico:
Passo 1
Esta função, é definida por duas partes, então ao esboçarmos o gráfico devemos representar a parábola até o valor de for e a partir dele, temos a reta onde cada valor de é dado pelo mesmo valor de .
Para esboçarmos o gráfico de temos que para cada valor de temos um valor de que é o seu quadrado menos uma unidade, então basta pensar no gráfico de e “descer” a parábola em uma unidade no eixo .
Passo 2
Então temos o gráfico:
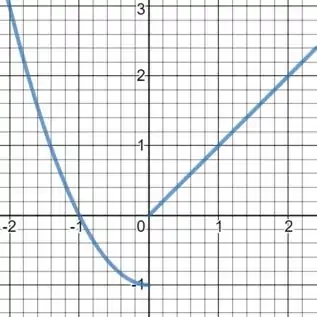
Resposta
Ei, a resposta está no passo a passo :)