Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 20

Encontre a equação cartesiana para a curva descrita pela equação polar dada.

r 2 sen ⁡ 2 θ = 1

Passo 1

Faalaee!! Vamos resolver uma questãozinha???

Bom... Queremos encontrar a equação cartesiana (ou seja, uma y = f x ) para a curva descrita pela seguinte equação polar:

r 2 sen ⁡ 2 θ = 1

Para isso, a gente precisa saber que podemos relacionar as coordenadas cartesianas x , y com as coordenadas polares r , θ da seguinte forma:

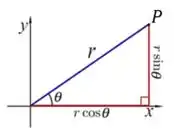
Veja que o ponto P pode ser dado tanto em coordenadas cartesianas como em coordenadas polares.

Veja também que temos um triângulo retângulo. Assim, podemos fazer algumas relações!! 😉

Passo 2

Pra começar, a gente vai precisar da seguinte relação trigonométrica:

s e n   2 θ = 2   s e n θ cos ⁡ θ

Assim, substituindo essa relação na equação dada no enunciado, temos:

r 2   2 s e n θ cos ⁡ θ = 1 ∴

2 r 2 s e n θ cos ⁡ θ = 1

Aí a gente pode fazer assim:

2   r c o s   θ ⋅ r s e n   θ = 1

Analisando o triângulo retângulo no passo 1, temos as seguintes relações:

x = r cos ⁡ θ

y = r   s e n   θ

Dessa forma, substituindo na nossa equação, temos:

2 x y = 1 ∴

y = 1 2 x

Prontinho😊

Resposta

y = 1 2 x

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre as coordenadas cartesianas do ponto.a) 2 ,3 π 2 b) 2 , π 4 c) - 1 ,- π 6
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre as coordenadas cartesianas do ponto.a) 4 , 4 π 3 b) - 2 , 3 π 4 c) - 3 ,- π 3
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 9 a 32 esboçar o gráfico das curvas dadas em coordenadas polares.
Nos exercícios 33 a 3 7 , encontrar o comprimento de arco da curva dada.