Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.3 - Ex. 4
Marque o ponto cujas coordenadas polares são dadas. A seguir, encontre as coordenadas cartesianas do ponto.
a)
b)
c)
Passo 1
Falaee, beleza?? Bom... o enunciado nos deu os seguintes pontos dados em coordenadas polares :
a)
b)
c)
Queremos encontrar as coordenadas cartesianas de cada um desses pontos.
Para isso, a gente tem que ter em mente que um ponto pode ser dado da seguinte forma:
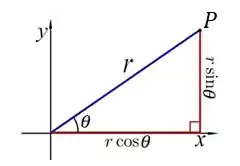
Assim, basta aplicarmos os valores de dados na seguinte relação:
Agora bora lá!! 😉
Passo 2
Vamos para o primeiro ponto .
Esse é o ponto de raio e ângulo igual a radianos ou :
Aí pra achar as equações cartesianas é só a gente fazer:
Já que e , temos:
E
As coordenadas cartesianas então são:
Passo 3
Agora vamos para o ponto .
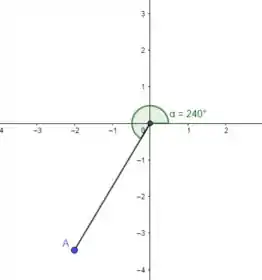
Aqui a gente tem raio e radianos ou :
Aqui o raio tá invertido (por causa do sinal), por isso que o ângulo muda no desenho.
Pra coordenadas cartesianas agora:
E
Fica o ponto assim então:
Passo 4
Por fim, vamos fazer para o ponto .
Agora a gente tem raio (só que invertido) e ângulo radianos ou :
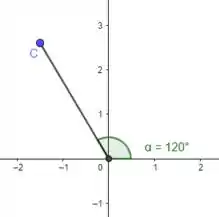
(Fica porque o raio tá invertido)
Aí em coordenadas cartesianas:
E
O ponto então é: