Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 32
Encontre uma equação para a cônica que satisfaz as condições dadas
Parábola, vértice , diretriz
Passo 1
Fala galera. Tudo belezinha?
Vamos começar a resolver a questão!
A questão pede para encontrar a equação de uma parábola com vértice em e diretriz . Para resolver esse problemas, podemos seguir os seguintes passos.
- Utilizar a equação da parábola para identificarmos o valor de .
- Devermos determinar a orientação da parábola com os dados fornecidos pelo anunciado.
- Aplicar a forma padrão da equação da parábola para vertical ou horizontal,
- Ao escrever a equação final, substituir os valores e finalizamos com a equação da parábola.
Vamos começar a trabalhar, mão na massa!
Passo 2
Nessa questão, nos foi dado o nome da cônica, seu vértice e diretriz para encontrarmos sua equação.
Bom, sabemos que é uma parábola, e parábolas tem equações nos formatos
Ou
.
Passo 3
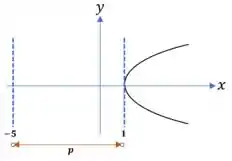
A diretriz é uma linha vertical representada pela equação . Isso significa que todos os pontos da parábola estão a uma distância constante (denominada "distância focal") da diretriz.
A forma da parábola será:
Passo 4
Para uma parábola que se abre horizontalmente com vértice em e foco em , a equação padrão é
onde:
- O vértice da parábola é .
- é o foco da parábola.
- é a distância entre o vértice e o foco (e também entre o vértice e a diretriz).
é a distância horizontal entre o vértice e a reta da diretriz.
Passo 5
Com todos os termos.
Como o vértice é , não temos um deslocamento no eixo de uma unidade, portanto
Com isso, nossa equação fica:
Passo 6
O gráfico formado foi
Resposta
