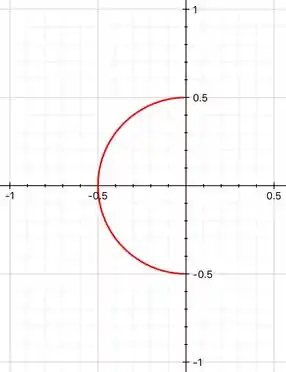
Desenhe um esboço do gráfico da equação:
Passo 1
Para esboçar o gráfico de uma equação, precisamos saber o tipo de gráfico que ela representa. Para isso, observamos as potências de x e de y na equação e comparamos com as equações básicas que nós sabemos, como , , , , entre outras que conhecemos. Depois é só deslocar o gráfico base em a unidades para a esquerda, para a direita, para baixo ou para cima, respectivamente, quando substituímos x por ou y por , e ainda alongar ou contrair o gráfico caso tenha alguma constante multiplicando as variáveis. Nesse último caso, substituímos valores para saber como a constante alterou o gráfico base.
Passo 2
Para descobrirmos que equação base usaremos, vamos precisar desenvolver essa equação. Elevando os dois lados ao quadrado, temos,
Passo 3
Como podemos ver, nossa equação é a metade da esquerda de uma circunferência de raio e centrada na origem.
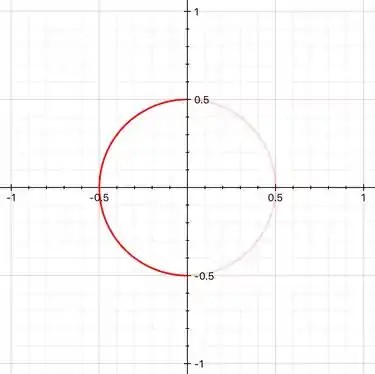
Resposta