Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 30
Encontre uma equação da forma cujo gráfico se adeque razoavelmente com o da figura abaixo. Confira seu trabalho com um recurso gráfico.
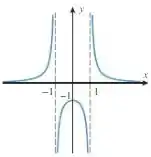
Passo 1
Vamos olhar para o gráfico de novo:
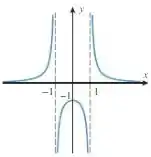
Para que se adeque a esse gráfico, precisamos que ele tenha as mesmas assíntotas verticais e horizontais.
Pelo gráfico, vemos duas assíntotas verticais: uma em e outra em . Como as assíntotas vão acontecer quando tivermos uma divisão por , esses valores de devem tornar o denominador igual a . Ou seja, e devem ser as raízes de .
Com isso, podemos escrever um polinômio que contenha essas raízes no denominador. Sabendo que um polinômio pode ser escrito na forma fatorada:
Onde são as raízes desse polinômio. Temos que o nosso denominador:
Assim, temos até agora que:
Passo 2
Para achar , vamos usar a informação de que o gráfico passa pelo ponto , substituindo esse ponto:
Prontinho, nossa função será:
O gráfico dela é:
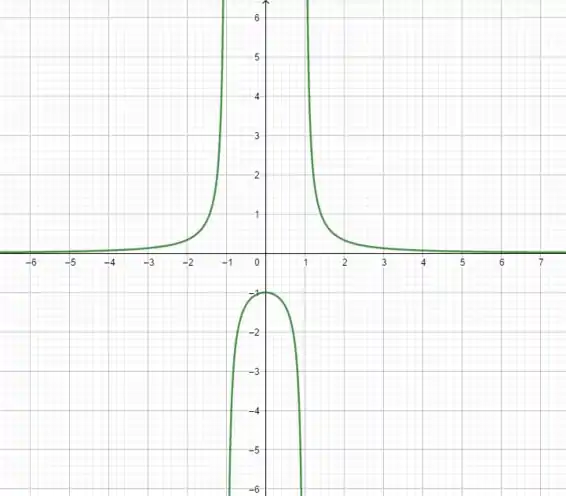
Igualzinha ao do problema! Hehe