Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.4 - Ex. 22
Encontre todas as soluções da equação, com duas casas decimais de precisão.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente encontrar todas as soluções da equação:
com duas casas decimais de precisão.
Isso significa que precisamos encontrar os valores de que fazem essas duas funções, e , serem iguais.
A maneira mais fácil de fazer isso é analisando o gráfico dessas duas funções. Porque nós sabemos que elas serão iguais quando essas curvas se encontrarem no gráfico e aí nós conseguimos obter os valores de que fazem isso acontecer.
Lembrando que a função é uma função radical, que lembra o formato de uma parábola deitada no eixo , certo? E a função é uma função polinomial de terceiro grau, então ela vai cortar o eixo em três pontos. Essas são algumas informações caso você queira fazer o gráfico na mão, que é possível, mas utilizando uma ferramenta gráfica será mais fácil, tá?
Vamos lá!
Passo 2
Com o auxílio de um software, vamos plotar os gráficos das curvas e :
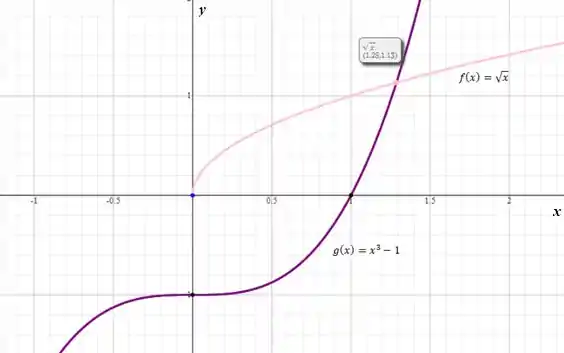
Observe que no ponto onde as curvas se encontram, a coordenada desse ponto de interseção (que é a soluções da equação) é aproximadamente . E como esse é o único ponto onde isso ocorre, a equação terá a solução única:
Podemos também encontrar as raízes da função igualando-a à zero, mas isso requer conhecimentos de matemática mais avançados.
Valeu, galera! Até a próxima! 😉