Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 68a
Encontre o valor exato de cada expressão.
(a)
Passo 1
O problema pede pra a gente encontrar o valor EXATO (sem pressão rs) da expressão . Antes de tudo, tenhamos em mente que , é a função que fornece o arco no intervalo cujo valor da secante é .
Além disso, vamos lembrar que a secante de um ângulo agudo em um triângulo retângulo nada mais é do que a razão da hipotenusa pelo cateto adjacente.Dessa forma, pra resolver a questão bem rápido, podemos pensar nela através de um triângulo retângulo onde a hipotenusa vale e um dos catetos vale :
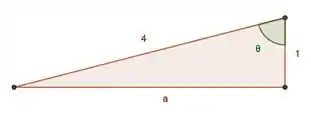
Assim, nesse triângulo sabemos que , dessa forma , e aí substituímos na expressão e ficamos com:
Passo 2
Agora é só fazermos um simples pitágoras:
Resposta
Exercícios de Livros Relacionados
Cada um dos Exercícios 11-16 apresenta o gráfico de uma função y = f ( x ) . Copie o gráfico e sobreponha-o à reta y = x . Em seguida, utilize a simetria com relação à reta y = x para adicionar o gráf
a) Faça o gráfico da função f x =1 - x ² ,0≤ x ≤ 1 ² . Que simetria o gráfico apresenta?
Cada um dos exercícios 19-24 apresenta a fórmula de uma função y = f ( x ) e mostra os gráficos de f e f - 1 . Determine uma fórmula para f - 1 em cada caso.
Cada um dos exercícios 19-24 apresenta a fórmula de uma função y = f ( x ) e mostra os gráficos de f e f - 1 . Determine uma fórmula para f - 1 em cada caso.
Cada um dos exercícios 19-24 apresenta a fórmula de uma função y = f ( x ) e mostra os gráficos de f e f - 1 . Determine uma fórmula para f - 1 em cada caso.