Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.6 - Ex. 65a
Encontre o valor exato de cada expressão.
(a)
Passo 1
Olá, meu querido aluno. Pronto para mais uma resolução?
Aqui iremos encontrar o valor exato para a expressão:
Para poder resolver, precisamos saber do que se trata o ou melhor dizendo o arco tangente. Em outras palavras, a função arco tangente é a função inversa da função tangente, o resultado de uma função arco tangente é o conjunto de valores dos ângulos que possuem a tangente .
Então:
Passo 2
Utilizando o círculo trigonométrico abaixo, podemos visualizar qual é o ângulo que possui a tangente igual a ;
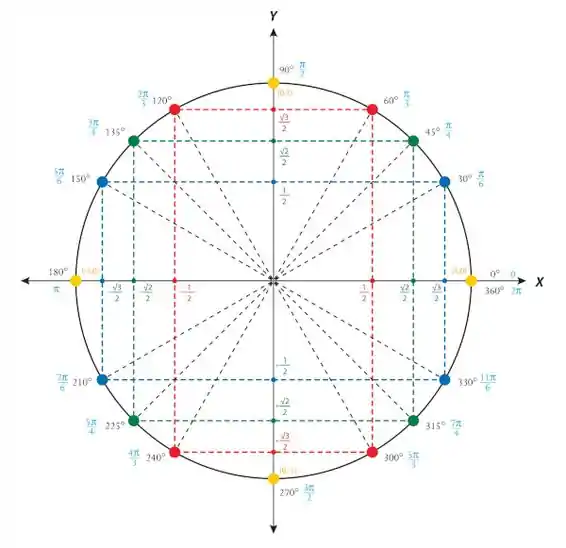
Como a função tangente é periódica, os seus valores se repetem a cada , sendo assim o conjunto de todos os valores que satisfazem a nossa equação é:
Resposta
Exercícios de Livros Relacionados
Simplifique: 9^()^(l o g _3 x)
Simplifique: l o g _2 ( e^()^(( l n 2 ) ( s e n x )) )
Crescimento populacional: A população de Glenbook é de 375.000 habitantes, e cresce à taxa de 2,25% por ano. Preveja quando a população chegará a 1 milhão.
Duplicando o seu dinheiro: Determine qual o tempo necessário para que um investimento de $500 dobre de valor em uma aplicação que rende 4,75% de juros compostos anualmente.
Radônio-222: A equação para o decaimento do gás radônio-222 é conhecida comoy = y oe - 0,18 t , sendo t expresso em dias. Qual o tempo necessário para que uma amostra de ar em um recipiente hermético