Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.5 - Ex. 8

Encontre o vértice, o foco e a diretriz da parábola e esboce seu gráfico.

8. y + 12 x - 2 x 2 = 16

Passo 1

Nessa questão, nós temos uma parábola de equação y + 12 x - 2 x 2 = 16   e precisamos encontrar seu vértice, foco e diretriz. Para isso, vamos primeiro reescrever esta equação da seguinte forma:

y + 12 x - 2 x 2 = 16

y = 2 x 2 - 12 x + 16

y = 2 ( x 2 - 6 x ) + 16

y = 2 ( x 2 - 6 x + 9 - 9 ) + 16

y = 2 x 2 - 6 x + 9 - 18 + 16

y = 2 x - 3 2 - 2

y + 2 = 2 x - 3 2

x - 3 2 = 1 2   ( y + 2 )

Lembre que a fórmula geral de uma parábola é ( x - h ) 2 = 4 p ( y - k ) , e que seu foco é da forma f = ( h , p + k )

Nesse caso k = - 2 ,     h = 3

4 p = 1 / 2 , então p = 1 / 8

O foco da parábola será f = 3 ,   - 15 8

Passo 2

A diretriz de uma parábola pode ser encontrada fazendo y = - p +k , portanto: y = - 1 7 / 8 é nossa diretriz.

Passo 3

Agora olhando novamente para a fórmula geral ( x - h ) 2 = 4 p ( y - k ) ,   percebemos que k = - 2   e     h = 3 . O vértice de uma parábola pode ser descrito como V = h , k , então nosso vértice é V = ( 3 , - 2 )

Passo 4

Agora que já temos todas essas informações podemos fazer um esboço do gráfico, note que como o termo que está ao quadrado é x , essa é uma parábola no eixo X .   O gráfico fica assim:

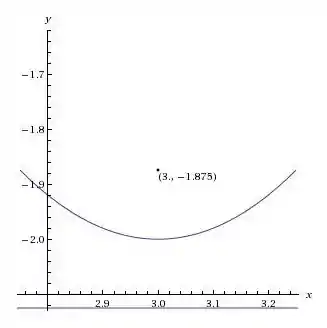
Resposta

V = ( 3 , - 2 )

f = 3 ,   - 15 8

Diretriz: y = - 1 7 / 8

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe um esboço do gráfico da equação: y = sqrt(x - 1)
Desenhe um esboço do gráfico da equação: y = sqrt(x + 4)
Desenhe um esboço do gráfico da equação: y = - sqrt(x + 4)
Desenhe um esboço do gráfico da equação: y = - sqrt(x - 1)
Desenhe um esboço do gráfico da equação: y^2 = x + 4