Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.5 - Ex. 11

Encontre os vértices e os focos da elipse e esboce seu gráfico.

11-

x 2 9 + y 2 5 = 1

Passo 1

Olá, meu amigo. Vou te ajudar a resolver essa atividade. A gente tem a equação da elipse:

x 2 9 + y 2 5 = 1

E a partir dela a gente precisa encontrar o foco e os vértices. Vamos fazer isso utilizando a equação geral da elipse.

( x - x 0 ) 2 a 2 + y - y 0 2 b 2 = 1

O foco está em:

( ± c ,   0 )

E o vértice:

± a , 0

E

c 2 = a 2 - b 2

Então comparando a nossa equação a geral, a gente consegue resolver essa atividade aqui.

Passo 2

Pela equação característica da elipse temos:

( x - x 0 ) 2 a 2 + y - y 0 2 b 2 = 1

Logo:

a 2 = 9

a = 3

b 2 = 5

b = 5

Os vértices da elipse estarão então em:

( ± 3,0 )

( 0 , ± 5 )

Além de x 0 = y 0 = 0 o que nos diz que a elipse está centrada na origem.

Assumindo somente os valores positivos para formar a equação.

Passo 3

Como a > b então os pontos de foco da elipse estarão sobre o eixo x , e terão valores iguais a:

c = a 2 - b 2

c = 9 - 5

c = 4

c = ± 2

Logo elas estarão a mais e menos 2 posições da origem. Ou seja, em

c 1 = ( 2,0 )

c 2 = ( - 2,0 )

Passo 4

O gráfico dessa função será igual a:

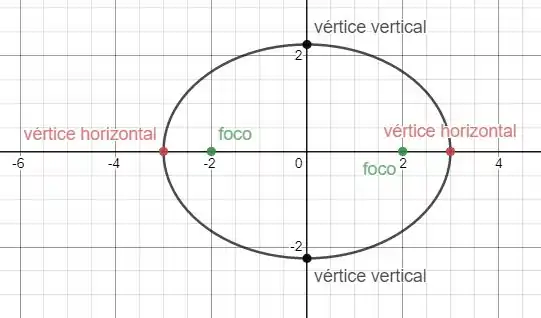
Geramos o gráfico utilizando o GeoGebra, para facilitar as nossas vidas !!!

Resposta

Vértices verticais:

( 0 , ± 5 )

Vértices horizontais:

( ± 3,0 )

Focos:

( ± 2,0 )

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhe um esboço do gráfico da equação: x = (1)/(2) sqrt(1 - 4 * y^2)
Desenhe um esboço do gráfico da equação: y = - sqrt(1 - x^2)
Desenhe um esboço do gráfico da equação: x = - (1)/(2) sqrt(1 - 4 * y^2)
Desenhe um esboço do gráfico da equação: x * y = 2
Desenhe um esboço do gráfico da equação: 4 * x^2 + 4 * y^2 = 1