Enunciado
Cálculo - Thomas - Vol 2- Ed: 12º - Capítulo 11.Exercícios adicionais e avançados - Ex. 23
Epicicloides. Quando um círculo gira externamente ao longo da circunferência de um segundo círculo fixo, qualquer ponto na circunferência do círculo que gira descreve uma epicicloide, conforme mostrado aqui. Suponha que o círculo fixo tenha seu centro na origem e raio.
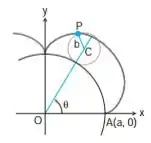
Seja o raio do círculo que gira e seja a posição inicial do ponto traçado . Encontre equações paramétricas para a epicicloide, utilizando como parâmetro o ângulo a partir do
eixo positivo até a reta que passa pelos centros dos círculos.
Passo 1
Oi galerinha, este exercício é mais teórico, mas vamos resolve-lo juntos. Vamos lá!
Podemos observar que quando o círculo gira, o centro descreve um círculo centrado em e de raio . Como é a medida do ângulo que o semieixo positivo faz com a semirreta no sentido positivo, temos que:
Seja o sistema obtido por uma rotação positiva de ângulo do sistema seguida de uma translação dos eixos que leva o ponto no ponto , onde:
E:
são as coordenadas de no sistema .
Passo 2
Se considerarmos que é a medida do ângulo que a semirreta faz com a semirreta no sentido positivo, então é o ângulo que o semieixo positivo faz com a semirreta no sentido positivo. Assim:
são coordenadas de no sistema . Logo, pelas seguintes equações de mudança de coordenadas:
Onde e são coordenadas de no sistema . Então:
Substituindo , obtemos as seguintes equações paramétricas da epiciclóide em função apenas do parâmetro :
Tchau pessoal.